题目内容
已知集合A={x||2x-1|≤3},B={x|log0.5x≥a},且B?A,则实数a的取值范围是( )
| A、a≥-1 | B、a≥1 |
| C、a≤-1 | D、a≤1 |
考点:对数函数的单调性与特殊点,指数函数单调性的应用
专题:函数的性质及应用,集合
分析:结合指数的运算性质解绝对值不等式|2x-1|≤3可求出集合A,解对数不等式求出集合B,进而根据集合的真包含的定义构造关于实数a的不等式,解不等式可得实数a的取值范围.
解答:
解:∵集合A={x||2x-1|≤3}={x|-3≤2x-1≤3}={x|-2≤2x≤4}={x|x≤2}
B={x|log0.5x≥a}={x|0<x≤2-a},
∵B?A,
∴0<2-a≤2,
∴-a≤1,
∴a≥-1,
故选:A
B={x|log0.5x≥a}={x|0<x≤2-a},
∵B?A,
∴0<2-a≤2,
∴-a≤1,
∴a≥-1,
故选:A
点评:本题考查的知识点是对数函数的单调性与特殊点,指数函数的单调性的应用,绝对值不等式和集合的包含关系,难度中档.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
若
,z=x+2y的最大值是3,则a的值是( )
|
| A、1 | B、-1 | C、0 | D、2 |
函数f(x)=2x-1+log2x的零点所在的一个区间是( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
| D、(1,2) |
 如图:α∩β=AB,PC⊥α,PD⊥β,C、D是垂足,试判断直线AB与CD的位置关系?并证明你的结论.
如图:α∩β=AB,PC⊥α,PD⊥β,C、D是垂足,试判断直线AB与CD的位置关系?并证明你的结论.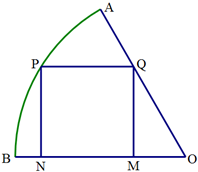 如图,在半径为
如图,在半径为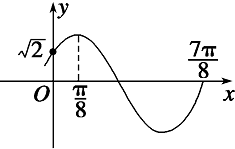 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<