题目内容
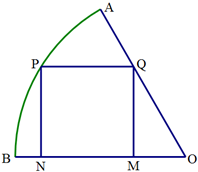 如图,在半径为
如图,在半径为| 3 |
(1)设∠POB=θ,求y表示成θ的函数;
(2)请根据你在(1)中写出的函数解析式,求出y的最大值.
考点:同角三角函数基本关系的运用,函数解析式的求解及常用方法,三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:(1)直接利用解直角三角形知识求出关系式.注意定义域的范围.
(2)利用(1)的结论对关系式进行恒等变换,变换成正弦型函数,最后利用定义域求函数的值域.
(2)利用(1)的结论对关系式进行恒等变换,变换成正弦型函数,最后利用定义域求函数的值域.
解答:
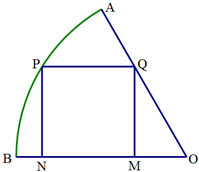 (本题满分12分)
(本题满分12分)
解:(1)在Rt△PON中,∠PNO=90°,∠POB=θ,PO=
所以PN=
sinθ,ON=
cosθ
在Rt△QMO中,∠QMO=90°,∠QON=60°,QM=PN=
sinθ
所以OM=
=
=sinθ
所以:MN=ON-OM=
cosθ-sinθ
所以y=PN•NM=
sinθ(
cosθ-sinθ)
即:y=3sinθcosθ-
sin2θ(0<θ<
)
(2)由(1)得
y=3sinθcosθ-
sin2θ
=
sin2θ-
=
(sin2θcos
+cos2θsin
)-
=
sin(2θ+
)-
由于:0<θ<
<2θ+
<
<sin(2θ+
)≤1
所以:0<
sin(2θ+
)-
≤
即:0<y≤
最大值为:
 (本题满分12分)
(本题满分12分)解:(1)在Rt△PON中,∠PNO=90°,∠POB=θ,PO=
| 3 |
所以PN=
| 3 |
| 3 |
在Rt△QMO中,∠QMO=90°,∠QON=60°,QM=PN=
| 3 |
所以OM=
| QM |
| tan∠QON |
| ||
| tan60° |
所以:MN=ON-OM=
| 3 |
所以y=PN•NM=
| 3 |
| 3 |
即:y=3sinθcosθ-
| 3 |
| π |
| 3 |
(2)由(1)得
y=3sinθcosθ-
| 3 |
=
| 3 |
| 2 |
| 3 |
| 1-cos2θ |
| 2 |
=
| 3 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
=
| 3 |
| π |
| 6 |
| ||
| 2 |
由于:0<θ<
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
所以:0<
| 3 |
| π |
| 6 |
| ||
| 2 |
| ||
| 2 |
即:0<y≤
| ||
| 2 |
最大值为:
| ||
| 2 |
点评:本题考查的知识要点:解直角三角形和三角关系式的恒等变换,利用定义域求函数的值域,属于基础题型.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
已知实数满足x2+y2=4,那么3y-4x的最大值为( )
| A、10 | ||
| B、8 | ||
| C、6 | ||
D、
|
已知集合A={x||2x-1|≤3},B={x|log0.5x≥a},且B?A,则实数a的取值范围是( )
| A、a≥-1 | B、a≥1 |
| C、a≤-1 | D、a≤1 |
 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录用茎叶图表示(如图),则该赛季发挥更稳定的运动员是
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录用茎叶图表示(如图),则该赛季发挥更稳定的运动员是


