Question

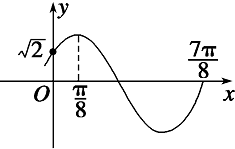函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜

π

2

）的一段图象（如图所示）
（1）求其解析式．
（2）令g（x）=

f2(x)-2f(x)+2

f(x)-1

，当x∈[0，

π

4

]时，求g（x）的最大值．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正切函数的值域

专题：三角函数的图像与性质

分析：（1）直接利用函数的图象，求出函数的周期，得到ω，然后利用函数经过的点求出φ，即可得到其解析式．
（2）化简g（x）=

f2(x)-2f(x)+2

f(x)-1

，通过换元法，结合正弦函数的单调性即可求解当x∈[0，

π

4

]时，g（x）的最大值．

解答： 解：（1）设函数f（x）的周期为T，
则由图知

3

4

T=

7π

8

-

π

8

=

3π

4

，∴T=π，
∴ω=

2π

π

=2，
∴f（x）=Asin（2x+ϕ）
将点（

7π

8

，0）代入得sin（2×

7π

8

+ϕ）=0，
∴

7π

4

+φ=2kπk∈Z，
∴φ=-

7π

4

+2kπk∈Z．
∵|ϕ|＜

π

2

，
∴φ=

π

4

．
∴f（x）=Asin（2x+

π

4

）．
将点（0，

2

）代入得

2

=Asin

π

4

，∴A=2，
∴f（x）=2sin（2x+

π

4

），
（2）g（x）=

f2(x)-2f(x)+2

f(x)-1

=

(f(x)-1)2+1

f(x)-1

=(f(x)-1)+

1

f(x)-1

，
设m=f（x）-1=2sin（2x+

π

4

）-1，则y=m+

1

m

，
当x∈[0，

π

4

]时，2x+

π

4

∈[

π

4

，

3π

4

]，sin2x+

π

4

∈[

2

2

，1]，m∈[

2

-1，1]，
y=m+

1

m

在[

2

-1，1]为减函数，
当m=

2

-1，即2sin（2x+

π

4

）-1=

2

-1，即x=0或x=

π

4

时，g（x）取得最大值2

2

．

点评：本题考查三角函数的解析式的求法，函数的最值的求法，考查转化思想以及计算能力．