题目内容
若
，z=x+2y的最大值是3，则a的值是（ ）
|
| A、1 | B、-1 | C、0 | D、2 |
考点：数列的求和
专题：不等式的解法及应用
分析：作出不等式表示的平面区域，明确目标函数的几何意义，根据z=x+2y的最大值为3，即可求a的值．
解答：
解：作出不等式表示的平面区域，如图
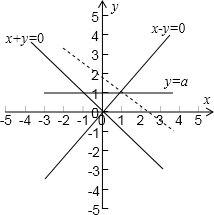
z=x+2y的几何意义是直线y=-
纵截距的一半
由
，可得x=y=a，根据图形可知在（a，a）处，z=x+2y的最大值为3
∴a+2a=3
∴a=1
故选A．
z=x+2y的几何意义是直线y=-
| 1 |
| 2 |
由
|
∴a+2a=3
∴a=1
故选A．
点评：本题考查线性规划知识，考查求函数的最值，正确作出不等式表示的平面区域，明确目标函数的几何意义是关键．
练习册系列答案
阅读快车系列答案
相关题目
已知方程
x2+
x+
=0，其中
，
，
是非零向量，且
，
不共线，则该方程（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| A、至多有一个解 |
| B、至少有一个解 |
| C、至多有两个解 |
| D、可能有无数多个解 |
已知a1=1，an+1-an=n，则a6=（ ）
| A、16 | B、15 | C、14 | D、13 |
已知实数满足x2+y2=4，那么3y-4x的最大值为（ ）
| A、10 | ||
| B、8 | ||
| C、6 | ||
D、
|
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录用茎叶图表示（如图），则该赛季发挥更稳定的运动员是已知集合A={x||2x-1|≤3}，B={x|log0.5x≥a}，且B?A，则实数a的取值范围是（ ）
| A、a≥-1 | B、a≥1 |
| C、a≤-1 | D、a≤1 |