题目内容
已知函数f(x)=ex-ax2(a∈R).
(Ⅰ)求函数f(x)在点P(0,1)处的切线方程;
(Ⅱ)若函数f(x)为R上的单调递增函数,试求a的取值范围.
(Ⅰ)求函数f(x)在点P(0,1)处的切线方程;
(Ⅱ)若函数f(x)为R上的单调递增函数,试求a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)求出函数的导数,根据导数的几何意义即可求函数f(x)在点P(0,1)处的切线方程;
(Ⅱ)根据函数单调性和导数之间的关系即可得到结论.
(Ⅱ)根据函数单调性和导数之间的关系即可得到结论.
解答:
解:(Ⅰ)∵f(x)=ex-ax2(a∈R).
∴f′(x)=ex-2ax,
∴f′(0)=1,
即f(x)在点P(0,1)处的切线方程为y-1=x,即y=x+1.
(Ⅱ)要使函数f(x)为R上的单调递增函数,
则f′(x)=ex-2ax≥0恒成立,
①当x>0时,2a≤
成立,
设g(x)=
,则g′(x)=
,
由g′(x)=0得x=1,
当x>1时,g′(x)>0,此时函数单调递增,
当x<1时,g′(x)<0,此时函数单调递减.
∴g(x)min=g(1)=e,∴a≤
.
②x<0时,2a≥
成立,
∵
<0,∴2a≥0,则a≥0;
又a=0,f′(x)=ex≥0恒成立;
综上,若函数f(x)为R上的单调递增函数,则0≤a≤
.
∴f′(x)=ex-2ax,
∴f′(0)=1,
即f(x)在点P(0,1)处的切线方程为y-1=x,即y=x+1.
(Ⅱ)要使函数f(x)为R上的单调递增函数,
则f′(x)=ex-2ax≥0恒成立,
①当x>0时,2a≤
| ex |
| x |
设g(x)=
| ex |
| x |
| ex(x-1) |
| x2 |
由g′(x)=0得x=1,
当x>1时,g′(x)>0,此时函数单调递增,
当x<1时,g′(x)<0,此时函数单调递减.
∴g(x)min=g(1)=e,∴a≤
| e |
| 2 |
②x<0时,2a≥
| ex |
| x |
∵
| ex |
| x |
又a=0,f′(x)=ex≥0恒成立;
综上,若函数f(x)为R上的单调递增函数,则0≤a≤
| e |
| 2 |
点评:本题主要考查导数的几何意义以及函数的单调性和导数之间的应用,求出函数的导数是解决本题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
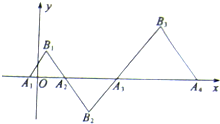 如图,在直角坐标平面xOy中,△AjBjAj+1(其中j=1,2,n,…)为正三角形,且满足
如图,在直角坐标平面xOy中,△AjBjAj+1(其中j=1,2,n,…)为正三角形,且满足