Question

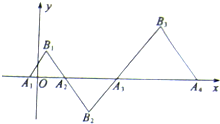如图，在直角坐标平面xOy中，△A_jB_jA_j+1（其中j=1，2，n，…）为正三角形，且满足

OA1

=（-

1

4

，0），

AjAj+1

=（2j-1，0），记点B_j的坐标为（x_j，y_j）．
（Ⅰ）计算x₁•x₂•x₃，并猜想x_n的表达式；
（Ⅱ）请用数学归纳法证明你的猜想．

Answer 1

考点：数学归纳法,平面向量数量积的运算

专题：点列、递归数列与数学归纳法

分析：（Ⅰ）依题意知，点A₁（-

1

4

，0），且

A1A2

=（1，0），可求得点A₂（

3

4

，0），于是可得x₁=

- 1 4 + 3 4

2

=

1

4

，同理可得x₂=

9

4

，x₃=

25

4

，于是猜想，x_n=

(2n-1)2

4

；
（Ⅱ）利用数学归纳法证明：①当n=1时，由（Ⅰ）知x₁=

1

4

=

(2×1-1)2

4

，命题成立，②假设n=k时命题成立，去推证n=k时命题成立即可．

解答： （Ⅰ）解：根据题意知，点A₁（-

1

4

，0），且

A1A2

=（1，0），所以点A₂（

3

4

，0），
所以x₁=

- 1 4 + 3 4

2

=

1

4

，…2分
同理x₂=

3 4 + 15 4

2

=

9

4

，…3分
x₃=

15 4 + 35 4

2

=

25

4

…4分
猜想，x_n=

(2n-1)2

4

…6分
（Ⅱ）证明：
①当n=1时，根据上一问的计算知，x₁=

1

4

=

(2×1-1)2

4

，所以命题成立；…8分
②假设n=k时命题成立，即x_k=

(2k-1)2

4

，
那么当n=k+1时，x_k+1=x_k+

| AkAk+1 |

2

+

| Ak+1Ak+2 |

2

=x_k+

2k-1

2

+

2k+1

2

=

(2k-1)2

4

+2k=

(2k+1)2

4

=

[2(k+1)-1]2

4

，
所以，当n=k+1时，命题成立…11分
由①②知，对任意n∈N^*命题都成立…12分

点评：本题考查数学归纳法，考查平面向量数量积的运算及递推关系式的应用，突出分析运算能力与推理证明能力的考查，属于难题．