题目内容
10.已知△ABC的三个内角A,B,C依次成等差数列,BC边上的中线AD=$\sqrt{7}$,AB=2,则S△ABC=( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
分析 由于△ABC的三个内角A、B、C成等差数列,且内角和等于180°,故 B=60°,ABD中,由余弦定理可得BD的长,进而利用三角形面积公式即可计算得解.
解答 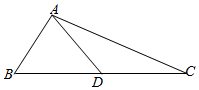 解:∵由于△ABC的三个内角A、B、C成等差数列,且内角和等于180°,
解:∵由于△ABC的三个内角A、B、C成等差数列,且内角和等于180°,
∴B=60°,
∵△ABD中,由余弦定理可得:AD2=AB2+BD2-2AB•BD•cosB,即:7=4+BD2-2BD,
∴BD=3或-1(舍去),可得:BC=6,
∴S△ABC=$\frac{1}{2}AB•BC•sinB$=$\frac{1}{2}×2×6×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
故选:C.
点评 本题考查等差数列的定义,余弦定理以及三角形面积公式的应用,求出B=60°,是解题的关键,属于基础题.

练习册系列答案
相关题目
18. 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )
 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )| A. | 49 | B. | 50 | C. | 99 | D. | 100 |
2.已知复数z=$\frac{2-i}{1+i}$(i为虚数单位),则在复平面内复数z所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
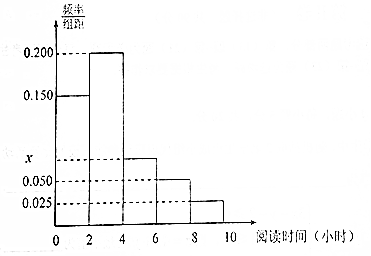 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图: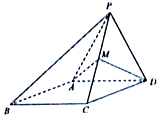 如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.