题目内容
15.已知点A(a,0),点P是双曲线C:$\frac{{x}^{2}}{4}$-y2=1右支上任意一点,若|PA|的最小值为3,则a=-1或2$\sqrt{5}$.分析 设P(x,y)(x≥2),则|PA|2=(x-a)2+y2=$\frac{5}{4}(x-\frac{4}{5}a)^{2}$+$\frac{1}{5}{a}^{2}$-1,分类讨论,利用|PA|的最小值为3,求出a的值.
解答 解:设P(x,y)(x≥2),则|PA|2=(x-a)2+y2=$\frac{5}{4}(x-\frac{4}{5}a)^{2}$+$\frac{1}{5}{a}^{2}$-1,
a>0时,x=$\frac{4}{5}$a,|PA|的最小值为$\frac{1}{5}{a}^{2}$-1=3,∴$a=2\sqrt{5}$,
a<0时,2-a=3,∴a=-1.
故答案为-1或2$\sqrt{5}$.
点评 本题考查双曲线的方程,考查距离公式的运用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知z是复数,且$\frac{z+2}{i}$=1+i,则z在复平面内对应的点的坐标为( )
| A. | (-3,1) | B. | (-3,-1) | C. | (1,-3) | D. | (-1,-3) |
10.已知△ABC的三个内角A,B,C依次成等差数列,BC边上的中线AD=$\sqrt{7}$,AB=2,则S△ABC=( )
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
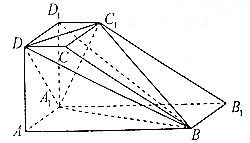 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.