题目内容
2.已知复数z=$\frac{2-i}{1+i}$(i为虚数单位),则在复平面内复数z所对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 直接利用复数代数形式的乘除运算化简,求出z所对应的点的坐标得答案.
解答 解:∵z=$\frac{2-i}{1+i}$=$\frac{(2-i)(1-i)}{(1+i)(1-i)}=\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i$,
∴在复平面内复数z所对应的点的坐标为($\frac{1}{2}$,-$\frac{3}{2}$),在第四象限.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
12.已知定义在(0,+∞)上的函数f(x)满足f(xy)+$\frac{1}{2}$-f(x)-f(y)=0,若一族平行线x=xi(i=1,2,…,n)分别与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xn,yn),且xi,2f(1),xn-i+1成等比数列,其中i=1,2,…,n,则$\frac{\sum_{i=1}^{n}{y}_{i}}{n}$=( )
| A. | 2n | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{n}{2}$ |
13.已知i是虚数单位,若复数z=3-4i,则计算$\frac{\overline{z}}{i}$的结果为( )
| A. | -4-3i | B. | 4-3i | C. | 4+3i | D. | -4+3i |
10.已知△ABC的三个内角A,B,C依次成等差数列,BC边上的中线AD=$\sqrt{7}$,AB=2,则S△ABC=( )
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
7.若变量x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x-y≤0}\\{x-2y+2≥0}\end{array}\right.$则$\frac{y}{x}$的最大值为( )
| A. | 1 | B. | 3 | C. | $\frac{3}{2}$ | D. | 5 |
14.已知x=${e}^{\frac{1}{6}}$(e为自然对数的底数),y=log52,z=log43,则下列结论正确的是( )
| A. | x<y<z | B. | y<z<x | C. | z<y<x | D. | z<x<y |
12.已知正项数列{an}中,a1=1,a2=2,$2{a_{n+1}}^2={a_{n+2}}^2+{a_n}^2$,则a6等于( )
| A. | 16 | B. | 8 | C. | 4 | D. | $2\sqrt{2}$ |
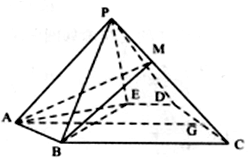 如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.