题目内容
1.已知等比数列{an}的各项均为正数,且log3a1+log3a3+log3a5+…+log3a19=10,则a10的值为( )| A. | 3 | B. | 6 | C. | 9 | D. | 18 |
分析 由对数运算法则得log3(a1×a3×…×a19)=10,从而${a}_{1}×{a}_{3}×…×{{a}_{19}}_{\;}^{\;}$=(a1×a19)5=${{a}_{10}}^{10}$=310,由此能求出a10.
解答 解:∵等比数列{an}的各项均为正数,
且log3a1+log3a3+log3a5+…+log3a19=10,
∴log3(a1×a3×…×a19)=10,
∴${a}_{1}×{a}_{3}×…×{{a}_{19}}_{\;}^{\;}$=(a1×a19)5=${{a}_{10}}^{10}$=310,
∴a10=3.
故选:A.
点评 本题考查等比数列的前10项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
12.已知定义在(0,+∞)上的函数f(x)满足f(xy)+$\frac{1}{2}$-f(x)-f(y)=0,若一族平行线x=xi(i=1,2,…,n)分别与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xn,yn),且xi,2f(1),xn-i+1成等比数列,其中i=1,2,…,n,则$\frac{\sum_{i=1}^{n}{y}_{i}}{n}$=( )
| A. | 2n | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{n}{2}$ |
9.椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右焦点分别为F1、F2,过F2作x轴的垂线交椭圆于点P,过P与原点O的直线交椭圆于另一点Q,则△F1PQ的周长为( )
| A. | 4 | B. | 8 | C. | $4+\sqrt{13}$ | D. | $2+\sqrt{13}$ |
13.已知i是虚数单位,若复数z=3-4i,则计算$\frac{\overline{z}}{i}$的结果为( )
| A. | -4-3i | B. | 4-3i | C. | 4+3i | D. | -4+3i |
10.已知△ABC的三个内角A,B,C依次成等差数列,BC边上的中线AD=$\sqrt{7}$,AB=2,则S△ABC=( )
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
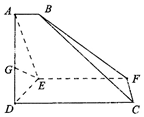 如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.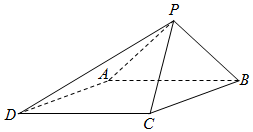 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,$AP=BP=\sqrt{2}$.