题目内容
设f:A→B是从A到B的一个映射,其中A=B={(x,y)|x∈R,y∈R},f:(x,y)→(x+y,xy),则A中(1,-2)的象是 ,B中(1,-2)的原象是 .
考点:映射
专题:计算题,函数的性质及应用
分析:根据对应法则和象、原象的坐标,即可得出结论.
解答:
解:由R到R的映射f:(x,y)→(x+y,xy),
x=1,y=-2,则x+y=-1,xy=-2,∴A中(1,-2)的象是(-1,-2);
设(1,-2)的原象是(x,y)
则x+y=1,xy=-2
解得:x=2,y=-1,或x=-1,y=2
故(1,-2)的原象是(2,-1)和(-1,2)
故答案为:(-1,-2);(2,-1)和(-1,2).
x=1,y=-2,则x+y=-1,xy=-2,∴A中(1,-2)的象是(-1,-2);
设(1,-2)的原象是(x,y)
则x+y=1,xy=-2
解得:x=2,y=-1,或x=-1,y=2
故(1,-2)的原象是(2,-1)和(-1,2)
故答案为:(-1,-2);(2,-1)和(-1,2).
点评:本题考查的知识点是映射的概念,其中根据对应法则和象的坐标,构造方程组是解答本题的关键.

练习册系列答案
相关题目
函数f(x)的定义域为R,f(-2)=2013,对任意x∈R都有f′(x)<2x成立,则不等式f(x)<x2+2009的解集是( )
| A、(-2,2) |
| B、(-2,+∞) |
| C、(-∞,-2) |
| D、(-∞,+∞) |
函数f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则有( )
| A、e2013f(-2013)<f(0),f(2013)>e2013f(0) |
| B、e2013f(-2013)<f(0),f(2013)<e2013f(0) |
| C、e2013f(-2013)>f(0),f(2013)>e2013f(0) |
| D、e2013f(-2013)>f(0),f(2013)<e2013f(0) |
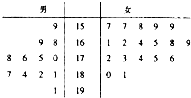 某县职工运动会将在本县一中运动场隆重召开,为了搞好接待工作,执委会在一中招募了12名男性志愿者和18名女性志愿者,调查发现,这30名志愿者的身高如图:(单位:cm)
某县职工运动会将在本县一中运动场隆重召开,为了搞好接待工作,执委会在一中招募了12名男性志愿者和18名女性志愿者,调查发现,这30名志愿者的身高如图:(单位:cm)