题目内容
已知椭圆的中心在原点,长轴长为6,一条准线方程为x=9,则该椭圆的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:设椭圆方程为
+
=1,(a>b>0),由已知条件推导出
,由此能求出该椭圆的标准方程.
| x2 |
| a2 |
| y2 |
| b2 |
|
解答:
解:∵椭圆的中心在原点,长轴长为6,
一条准线方程为x=9,
∴设椭圆方程为
+
=1,(a>b>0),
且
,解得a=3,c=1,b2=8,
∴该椭圆的标准方程为:
+
=1.
故选:B.
一条准线方程为x=9,
∴设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
且
|
∴该椭圆的标准方程为:
| x2 |
| 9 |
| y2 |
| 8 |
故选:B.
点评:本题考查椭圆的标准方程的求法,是基础题,解题时要认真审题,注意椭圆性质的灵活运用.

练习册系列答案
相关题目
椭圆
+y2=1上的点到直线x-y+6=0的最小距离是( )
| x2 |
| 3 |
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
设角θ的终边经过点(3,-4),则sin(
-θ)的值等于( )
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
函数f(x)=log2x+2x-6的零点所在的大致区间是( )
A、(
| ||
| B、(1,2) | ||
| C、(2,3) | ||
| D、(3,4) |
在△ABC中,若
=
,则△ABC的形状是( )
| a |
| cosA |
| b |
| cosB |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰或直角三角形 |
| D、等腰直角三角形 |
下列推理过程是类比推理的是( )
A、人们通过大量试验得出掷硬币出现正面的概率为
| ||
| B、科学家通过研究老鹰的眼睛发明了电子鹰眼 | ||
| C、通过检测溶液的pH值得出溶液的酸碱性 | ||
| D、数学中由周期函数的定义判断某函数是否为周期函数 |
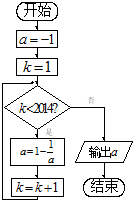
执行如图所示的程序框图所表达的算法,输出的结果为( )

| A、2 | ||
| B、1 | ||
C、
| ||
| D、-1 |