题目内容
4.在△ABC中,角A、B、C所对的边分别为a、b、c.已知sinB-sinC=$\frac{1}{4}$sinA,2b=3c,则cosA=$-\frac{1}{4}$.分析 由已知可得b=$\frac{3c}{2}$,又利用正弦定理可得b-c=$\frac{1}{4}$a,进而可得:a=2c,利用余弦定理即可解得cosA的值.
解答 解:在△ABC中,∵2b=3c,
∴可得:b=$\frac{3c}{2}$,
∵sinB-sinC=$\frac{1}{4}$sinA,
∴由正弦定理可得:b-c=$\frac{1}{4}$a,可得:$\frac{3c}{2}$-c=$\frac{1}{4}$a,整理可得:a=2c,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\frac{9{c}^{2}}{4}+{c}^{2}-4{c}^{2}}{2×\frac{3c}{2}×c}$=$-\frac{1}{4}$.
故答案为:$-\frac{1}{4}$.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
14.若点P在抛物线y=x2上,点Q(0,3),则|PQ|的最小值是( )
| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{\sqrt{11}}{2}$ | C. | 3 | D. | $\sqrt{5}$ |
15.设函数f(x)=2sin(ωx-$\frac{π}{3}$),已知f(α)=-2,f(β)=0,且|α-β|的最小值是$\frac{π}{4}$,现将y=f(x)的图象向左平移φ(φ>0)个单位,所得函数图象关于y轴对称,则φ的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{12}$ | D. | $\frac{5π}{12}$ |
12.执行如图的程序框图,如果输入的t∈[-1,π],则输出的S属于( )
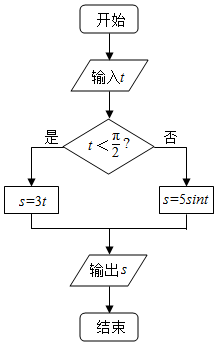

| A. | $[-3,\frac{3π}{2}]$ | B. | $[-5,\frac{3π}{2}]$ | C. | [-5,5] | D. | [-3,5] |
19.在△ABC中,角A、B、C所对的边分别为a、b、c.若c=3,$C=\frac{π}{3}$,且a+b=4,则△ABC的面积为( )
| A. | $\frac{7\sqrt{3}}{12}$ | B. | $\frac{7\sqrt{3}}{4}$ | C. | $\frac{7}{12}$ | D. | $\frac{5\sqrt{3}}{12}$ |
9.双曲线15y2-x2=15与椭圆$\frac{x^2}{25}+\frac{y^2}{9}$=1的( )
| A. | 焦点相同 | B. | 焦距相同 | C. | 离心率相等 | D. | 形状相同 |
13.点P(1,f(1))是曲线f(x)=x2-2$\sqrt{x}$$+\frac{1}{3}$上的点,设在点P处切线的倾斜角为α,则α的值( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |