题目内容
9．双曲线15y2-x2=15与椭圆$\frac{x^2}{25}+\frac{y^2}{9}$=1的（ ）| A． | 焦点相同 | B． | 焦距相同 | C． | 离心率相等 | D． | 形状相同 |
分析 分别求出双曲线与椭圆的焦点坐标、焦距和离心率，即可得出正确的结论．
解答 解：双曲线15y2-x2=15化为标准方程是y2-$\frac{{x}^{2}}{15}$=1，
它的焦点坐标是（0，±4），焦距是2c=8，离心率是e=4；
椭圆的标准方程是$\frac{x^2}{25}+\frac{y^2}{9}$=1，
它的焦点坐标为（±4，0），焦距是2c=8，离心率是e=$\frac{4}{5}$．
所以，它们的焦距相同．
故选：B．
点评 本题考查了双曲线与椭圆的简单几何性质的应用问题，是基础题目．
练习册系列答案
相关题目
19．
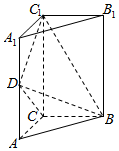如图，底面是直角三角形的直三棱柱ABC-A1B1C1中，$AC=BC=\frac{1}{2}A{A_1}=1$，D是棱AA1上的动点．
（1）证明：DC1⊥BC；
（2）求三棱锥C-BDC1的体积．
如图，底面是直角三角形的直三棱柱ABC-A1B1C1中，$AC=BC=\frac{1}{2}A{A_1}=1$，D是棱AA1上的动点．（1）证明：DC1⊥BC；
（2）求三棱锥C-BDC1的体积．
17．已知△ABC中，a=3，b=3$\sqrt{3}$，A=30°，则B等于（ ）
| A． | 30° | B． | 30°或150° | C． | 60° | D． | 60°或120° |
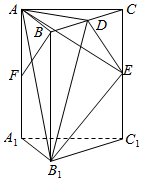如图，在直三棱柱ABC-A1B1C1中，AB⊥AC，AB=1，AC=$\sqrt{3}$，AA1=4，点D、E、F分别是棱BC、CC1、AA1的中点．
如图，扇形的半径为r cm，周长为20cm，问扇形的圆心角α等于多少弧度时，这个扇形的面积最大，并求出扇形面积的最大值．