题目内容
14.若点P在抛物线y=x2上,点Q(0,3),则|PQ|的最小值是( )| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{\sqrt{11}}{2}$ | C. | 3 | D. | $\sqrt{5}$ |
分析 由已知条件,设P(x,y),利用两点间距离公式,求出|PQ|,由此利用配方法能求出|PQ|的最小值.
解答 解:设P(x,y),
∵Q(0,3),
∴|PQ|=$\sqrt{{x}^{2}+(y-3)^{2}}$=$\sqrt{{y}^{2}-5y+9}$=$\sqrt{(y-\frac{5}{2})^{2}+\frac{11}{4}}$≥$\frac{\sqrt{11}}{2}$,
∴|PQ|的最小值是$\frac{\sqrt{11}}{2}$.
故选:B.
点评 本题考查两点间距离公式,考查配方法的运用,考查学生的计算能力,比较基础.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
4.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0,b>0)$的离心率为$\sqrt{5}$,则该双曲线的渐近线方程为( )
| A. | y=±2x | B. | $y=±\frac{1}{2}x$ | C. | $y=±\frac{1}{4}x$ | D. | y=±4x |
5.已知球O的一个内接三棱锥P-ABC,其中△ABC是边长为2的正三角形,PC为球O的直径,且PC=4,则此三棱锥的体积为( )
| A. | $\frac{2}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{2}$ | C. | $\frac{4}{3}\sqrt{6}$ | D. | $\frac{2}{3}\sqrt{6}$ |
9.已知点A是抛物线C:x2=2py(p>0)上一点,O为坐标原点,若以点M(0,8)为圆心,|OA|的长为半径的圆交抛物线C于A,B两点,且△ABO为等边三角形,则p的值是( )
| A. | $\frac{3}{8}$ | B. | 2 | C. | 6 | D. | $\frac{2}{3}$ |
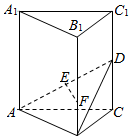 在正三棱柱ABC-A1B1C1中,AB=AA1=1,DC=DC1,AE=ED,F为BB1上任意一点,且FB1=3BF.
在正三棱柱ABC-A1B1C1中,AB=AA1=1,DC=DC1,AE=ED,F为BB1上任意一点,且FB1=3BF.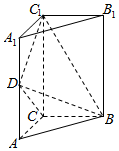 如图,底面是直角三角形的直三棱柱ABC-A1B1C1中,$AC=BC=\frac{1}{2}A{A_1}=1$,D是棱AA1上的动点.
如图,底面是直角三角形的直三棱柱ABC-A1B1C1中,$AC=BC=\frac{1}{2}A{A_1}=1$,D是棱AA1上的动点.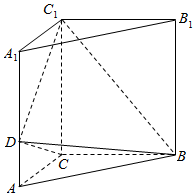 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{2}{5}$AA1,D是棱AA1上的点,且AD=$\frac{1}{4}$DA1.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{2}{5}$AA1,D是棱AA1上的点,且AD=$\frac{1}{4}$DA1.