题目内容
过抛物线y=-
x2的焦点作倾斜角为α的直线l交于A、B两点，若AB=8，则倾斜角α的值为 ．
| 1 |
| 4 |
考点：抛物线的标准方程
专题：圆锥曲线的定义、性质与方程
分析：依题意知，x2=-4y，其焦点坐标为F（0，-1），准线方程为y=1，利用抛物线的定义可知，点A与点B的纵坐标之和yA+yB=-6；将直线l的方程与抛物线方程联立，利用韦达定理可求得直线l的斜率，即tanα的值，从而可求α的值．
解答：
解：∵y=-
x2，
∴x2=-4y，
∴其焦点坐标为F（0，-1），准线方程为y=1；
又过焦点F的倾斜角为α直线l与抛物线x2=-4y交于A、B两点，且AB=8，
∴|yA-1|+|yB-1|=8，又yA＜0，yB＜0，
∴1-yA+1-yB=8，yA+yB=-6．
∵直线l的方程为：y+1=xtanα=kx，由
得：y2+（2+4k2）y+1=0，
显然△=（2+4k2）2-4＞0，
∴yA+yB=-（2+4k2）=-6，解得k=±1，即tanα=±1，
∴α=
或
．
故答案为：
或
．
| 1 |
| 4 |
∴x2=-4y，
∴其焦点坐标为F（0，-1），准线方程为y=1；
又过焦点F的倾斜角为α直线l与抛物线x2=-4y交于A、B两点，且AB=8，
∴|yA-1|+|yB-1|=8，又yA＜0，yB＜0，
∴1-yA+1-yB=8，yA+yB=-6．
∵直线l的方程为：y+1=xtanα=kx，由
|
显然△=（2+4k2）2-4＞0，
∴yA+yB=-（2+4k2）=-6，解得k=±1，即tanα=±1，
∴α=
| π |
| 4 |
| 3π |
| 4 |
故答案为：
| π |
| 4 |
| 3π |
| 4 |
点评：本题考查抛物线的标准方程，着重考查抛物线的定义的应用，考查直线与圆锥曲线的位置关系的综合应用，考查方程思想与韦达定理的应用，属于中档题．
练习册系列答案
相关题目
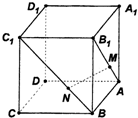如图所示，在正方体ABCD-A1B1C1D1中，点M、N分别在线段AB1、BC1上，且AM=BN．给出下列结论：