题目内容
已知定义域为D的函数f（x），若对任意x∈D，存在正数M，都有|f（x）|≤M成立，则称函数f（x）是定义域D上的“有界函数”．已知下列函数：
①f（x）=sinx•cosx+1；②f（x）=
；③f（x）=1-2x；④f（x）=lg
．
其中“有界函数”的个数是（ ）
①f（x）=sinx•cosx+1；②f（x）=
| 1-x2 |
| 1-x |
| 1+x |
其中“有界函数”的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：分别求四个函数的值域，对照“有界函数”的概念即可判断．
解答：
解：①中|f（x）|=|
sin2x+1|≤
为有界函数，
②中|f（x）|≤1 为有界函数，
③f（x）＜1 不是有界函数，
④f（x）=lg（-1+
）不是有界函数，
故选：B．
| 1 |
| 2 |
| 3 |
| 2 |
②中|f（x）|≤1 为有界函数，
③f（x）＜1 不是有界函数，
④f（x）=lg（-1+
| 2 |
| 1+x |
故选：B．
点评：本题以新“概念”为平台，考查学生知识迁移与理解能力，考查几种常见函数的值域，属于基础题．
练习册系列答案
优百分课时互动系列答案
相关题目
已知
=（-1，1），则|
|=（ ）
| a |
| a |
A、
| ||
| B、0 | ||
| C、1 | ||
D、-
|
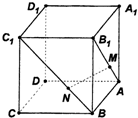如图所示，在正方体ABCD-A1B1C1D1中，点M、N分别在线段AB1、BC1上，且AM=BN．给出下列结论：①MN与A1C1相交；
②MN∥A1C1；
③MN与A1C1异面，
其中有可能成立的结论的个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
若α是第二象限的角，则角
所在的象限是（ ）
| α |
| 2 |
| A、第一象限 |
| B、第二象限 |
| C、第一象限或第二象限 |
| D、第一象限或第三象限 |
设集合U=﹛1，2，3，4﹜，A=﹛1，2﹜，B=﹛2，4﹜，则∁U（A∪B）=（ ）
| A、﹛2﹜ | B、﹛3﹜ |
| C、﹛1，4﹜ | D、﹛1，3，4﹜ |
若集合M={x|y=
}，且M∪N=M，则集合N可能是（ ）
| x |
| A、{-1，0，1} |
| B、{1，2} |
| C、{x|x≤1} |
| D、R |