题目内容
已知椭圆的中心为坐标原点,长轴在x轴上,其左、右焦点分别为F1、F2,过椭圆的左焦点且垂直于x轴的直线被椭圆截得的弦长为
,该椭圆的离心率为
,点P为椭圆上的一点.
(1)求椭圆的标准方程.
(2)若∠F1PF2=
,求三角形F1PF2的面积.
(3)若∠F1PF2为锐角,求P点的纵坐标的取值范围.
2
| ||
| 3 |
| ||
| 3 |
(1)求椭圆的标准方程.
(2)若∠F1PF2=
| π |
| 4 |
(3)若∠F1PF2为锐角,求P点的纵坐标的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆的方程为
+
=1(a>b>0),由已知条件得
=
,
=
,由此能求出椭圆的方程.(2)记|F1P|=m,|F2P|=n,由椭圆的定义得m+n=2
由余弦定理,得m2+n2-2mncos
=42,由此能求出三角形F1PF2的面积.
(3)设P点的坐标为(x0,y0),由F1(-2,0),F2(2,0),知
=(x0,
=(x0,由此能求出P点的纵坐标的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| 2b2 |
| a |
2
| ||
| 3 |
| c |
| a |
| ||
| 3 |
| 6 |
| π |
| 4 |
(3)设P点的坐标为(x0,y0),由F1(-2,0),F2(2,0),知
| F1P |
| F2P |
解答:
解:(1)设椭圆的方程为
+
=1(a>b>0),
由题意得
=
,
=
,
解得a2=6,b2=2,
故椭圆的方程为
+
=1.(3分)
(2)记|F1P|=m,|F2P|=n,
由椭圆的定义得m+n=2
,①
在△F1PF2中,由余弦定理,得m2+n2-2mncos
=42,②
将①平方后与②作差,得mn=8-4
,
∴S△F1F2P=
mnsin
=2
-2.(8分)
(3)设P点的坐标为(x0,y0),
由F1(-2,0),F2(2,0),知
=(x0,
=(x0,
由∠F1PF2为锐角,得
•
>0,即
+
-4>0,
又点P在椭圆上,故
+
=1,消去x0得
<1,
故所求P点纵坐标的取值范围是-1<y0<1且y0≠0.
| x2 |
| a2 |
| y2 |
| b2 |
由题意得
| 2b2 |
| a |
2
| ||
| 3 |
| c |
| a |
| ||
| 3 |
解得a2=6,b2=2,
故椭圆的方程为
| x2 |
| 6 |
| y2 |
| 2 |
(2)记|F1P|=m,|F2P|=n,
由椭圆的定义得m+n=2
| 6 |
在△F1PF2中,由余弦定理,得m2+n2-2mncos
| π |
| 4 |
将①平方后与②作差,得mn=8-4
| 2 |
∴S△F1F2P=
| 1 |
| 2 |
| π |
| 4 |
| 2 |
(3)设P点的坐标为(x0,y0),
由F1(-2,0),F2(2,0),知
| F1P |
| F2P |
由∠F1PF2为锐角,得
| F2P |
| F1P |
| x | 2 0 |
| y | 2 0 |
又点P在椭圆上,故
| ||
| 6 |
| ||
| 2 |
| y | 2 0 |
故所求P点纵坐标的取值范围是-1<y0<1且y0≠0.
点评:本题考查椭圆方程的求法,考查三角形面积的求法,考查点的纵坐标的取值范围的求法,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
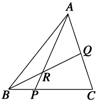
如图所示,P、Q分别在BC和AC上,BP:CP=2:5,CQ:QA=3:4,则
( )
| AR |
| RP |

| A、3:14 | B、14:3 |
| C、17:3 | D、17:14 |
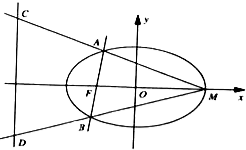 已知椭圆
已知椭圆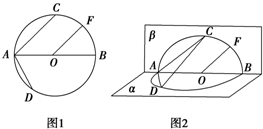 如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45°,F为
如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45°,F为 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,E为AB的中点,AB=8,AD=DC=4,∠PAD=60°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,E为AB的中点,AB=8,AD=DC=4,∠PAD=60°.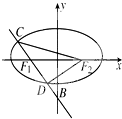 已知椭圆
已知椭圆