题目内容
已知直线l:mx-2y+2m=0(m∈R)和椭圆C:
+
=1(a>b>0),椭圆C的离心率为
,连接椭圆的四个顶点形成四边形的面积为2
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A,B两点,若以线段AB为直径的圆过原点O,求实数m的值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A,B两点,若以线段AB为直径的圆过原点O,求实数m的值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由离心率e=
及c2=a2-b2,得b=
a,再由2ab=2
可求a,b;
(Ⅱ)联立
,消去y得:(1+
)x2+2m2x+2m2-2=0.设A(x1,y1),B(x2,y2),由题意,得
•
=0,即x1x2+y1y2=0,由韦达定理代入可求m;
| ||
| 2 |
| ||
| 2 |
| 2 |
(Ⅱ)联立
|
| m2 |
| 2 |
| OA |
| OB |
解答:
解:(Ⅰ)由离心率e=
,得c=
a.
∵c2=a2-b2,∴b=
a.
又因为2ab=2
,所以a=
,b=1.
∴椭圆的标准方程为
+y2=1.
(Ⅱ) 联立
,消去y得:(1+
)x2+2m2x+2m2-2=0.
由△=4m4-4(1+
)(2m2-2)>0,得-
<m<
.
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
由题意,得
•
=0,即x1x2+y1y2=0,
∴x1x2+(
x1+m)(
x2+m)=0,即(1+
)x1x2+
(x1+x2)+m2=0,
∴(1+
)•
+
•
+m2=0.
解之,得m=±
,满足△>0,∴m=±
.
| ||
| 2 |
| ||
| 2 |
∵c2=a2-b2,∴b=
| ||
| 2 |
又因为2ab=2
| 2 |
| 2 |
∴椭圆的标准方程为
| x2 |
| 2 |
(Ⅱ) 联立
|
| m2 |
| 2 |
由△=4m4-4(1+
| m2 |
| 2 |
| 2 |
| 2 |
设A(x1,y1),B(x2,y2),则x1+x2=
| -2m2 | ||
1+
|
| 2m2-2 | ||
1+
|
由题意,得
| OA |
| OB |
∴x1x2+(
| m |
| 2 |
| m |
| 2 |
| m2 |
| 4 |
| m2 |
| 2 |
∴(1+
| m2 |
| 4 |
| 2m2-2 | ||
1+
|
| m2 |
| 2 |
| -2m2 | ||
1+
|
解之,得m=±
2
| ||
| 5 |
2
| ||
| 5 |
点评:该题考查椭圆的方程、性质,考查直线与椭圆的位置关系,韦达定理、判别式是该类题目常用知识,要熟练掌握.

练习册系列答案
相关题目
下面是一段“三段论”推理过程:若函数f(x)在(a,b)内可导且单调递增,则在(a,b)内,f′(x)>0恒成立.因为f(x)=x3在(-1,1)内可导且单调递增,所以在(-1,1)内,f′(x)=3x2>0恒成立.以上推理中( )
| A、大前提错误 |
| B、小前提错误 |
| C、结论正确 |
| D、推理形式错误 |
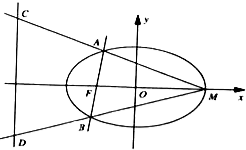 已知椭圆
已知椭圆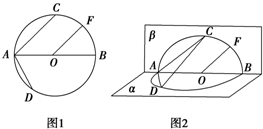 如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45°,F为
如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45°,F为 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,E为AB的中点,AB=8,AD=DC=4,∠PAD=60°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,E为AB的中点,AB=8,AD=DC=4,∠PAD=60°.