题目内容
已知函数f(x)=x2-2ax+2,x∈[-3,3].
(1)当a=-5时,求f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-3,3]上是单调函数.
[解析] (1)当a=-5时,f(x)=x2+10x+2=(x+5)2-23,x∈[-3,3],
又因为二次函数开口向上,且对称轴为x=-5,
所以当x=-3时,f(x)min=-19,
当x=3时,f(x)max=41.
(2)函数f(x)=(x-a)2+2-a2的图像的对称轴为x=a,因为f(x)在[-3,3]上是单调函数,
所以a≤-3或a≥3.

练习册系列答案
相关题目
在一次数学试验中,应用图形计算器采集到如下一组数据:
| x | -2.0 | -1.0 | 0 | 1.00 | 2.00 | 3.00 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=ax2+b D.y=a+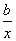
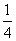 B.
B.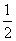
 D.
D.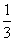
 那么f(-3)的值为( )
那么f(-3)的值为( )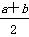 )>0.则( )
)>0.则( )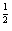 ,g(x)=(x
,g(x)=(x ,g(x)=x-3
,g(x)=x-3 <θ<π,且|cosθ|=
<θ<π,且|cosθ|= ,那么sin
,那么sin 的值为( )
的值为( ) B.-
B.- D.
D.