题目内容

在△ABC中，一定成立的等式是（　　）
A、asinB=bsinA
B、acosB=bcosA
C、atanB=btanA
D、asinA=bsinB
考点：正弦定理,两角和与差的正弦函数
专题：解三角形
分析：直接利用正弦定理判断即可．
解答： 解：在△ABC中，asinB=bsinA，可得：sinAsinB=sinBsinA，显然A的表达式一定成立．
故选：A．
点评：本题考查正弦定理的应用，三角形的求解，考查计算能力．
练习册系列答案
相关题目
已知集合A={x|x2-16＜0}，B={x|x2-4x+3＞0}，C={x|2x-m＞2}．
（Ⅰ）求A∩B；
（Ⅱ）若A⊆C，求实数m的取值范围．
在等差数列{an}中，已知a1=2，a2+a3=13，则a5=（　　）
A、13B、14C、15D、16
设a，b，c∈R，a2+（b+1）2+c2=3，则a+b+c的最小值是
 
．
幂函数y=xm2+m+1（m∈Z）的定义域是
 
，奇偶性是
 
．
已知椭圆C：
x2
a2
+
y2
b2
=1的左右焦点分别为F1，F2，点P（1，
3
2
）在椭圆C上，过点P的直线与圆x2+y2=1相切于点F2．求椭圆C的方程．
已知点A（6，1）B（1，3）C（3，1），求向量
AB
在向量
BC
上的投影．
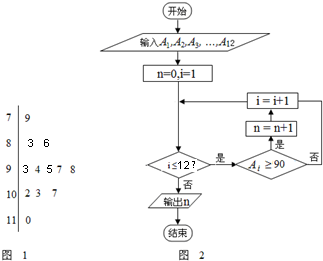图1是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到12次的考试成绩依次记为A1，A2，…，A12．图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是（　　）
A、8B、9C、10D、11
在△ABC中∠C=90°，AC=8，BC=6，以这个直角三角形的一条边所在的直线为轴旋转一周，求所得到的几何体的表面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网