题目内容
在△ABC中∠C=90°,AC=8,BC=6,以这个直角三角形的一条边所在的直线为轴旋转一周,求所得到的几何体的表面积.
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:以三条边分别为轴旋转,得到不同的圆锥或者圆锥的组合体,分别计算表面积.
解答:
解:(1)当以AC边所在的直线为轴旋转一周时,得到的几何体是一个圆锥,它的母线长为AB,底面圆半径为BC=6.由勾股定理,得
AB=
=
=10.
∴这时圆锥的表面积=π×6×10+π×62=60π+36π=96π.
(2)当以BC边所在直线为轴旋转一周时,得到的几何体也是一个圆锥,它的母线长为AB=10,底面圆半径为AC=8.
∴圆锥表面积=π×8×10+π×82=80π+64π=144π.
(3)当以AB边所在直线为轴旋转一周时,得到的几何体是底面是同圆,母线长分别是AC和BC的两个圆锥.
作CD⊥AB于D.则CD=
=
=4.8.
∵以AC为母线的圆锥的侧面积=π×4.8×8=
π,
以BC为母线的圆锥的侧面积=π×4.8×6=
π,
∴所求几何体的表面积=
π+
π=
π.
AB=
| AC2+BC2 |
| 82+62 |
∴这时圆锥的表面积=π×6×10+π×62=60π+36π=96π.
(2)当以BC边所在直线为轴旋转一周时,得到的几何体也是一个圆锥,它的母线长为AB=10,底面圆半径为AC=8.
∴圆锥表面积=π×8×10+π×82=80π+64π=144π.
(3)当以AB边所在直线为轴旋转一周时,得到的几何体是底面是同圆,母线长分别是AC和BC的两个圆锥.
作CD⊥AB于D.则CD=
| AC•BC |
| AB |
| 8×6 |
| 10 |
∵以AC为母线的圆锥的侧面积=π×4.8×8=
| 192 |
| 5 |
以BC为母线的圆锥的侧面积=π×4.8×6=
| 144 |
| 5 |
∴所求几何体的表面积=
| 192 |
| 5 |
| 144 |
| 5 |
| 336 |
| 5 |
点评:本题考查了三角形绕一边旋转得到的几何体表面积的计算,实质是圆锥的表面积的计算;关键是明确圆锥的母线长以及底面半径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,一定成立的等式是( )
| A、asinB=bsinA |
| B、acosB=bcosA |
| C、atanB=btanA |
| D、asinA=bsinB |
已知
=(cosα,1,sinα),
=(sinα,1,cosα),且sinα≠cosα,则向量
+
与
-
的夹角是( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、0° | B、30° |
| C、60° | D、90° |
关于x的方程x2-mx+16=0在x∈[1,10]上有实根,则实数m的取值范围是( )
| A、[8,17] | ||
| B、(1,8] | ||
| C、(-∞,-8]∪[8,+∞) | ||
D、[8,
|
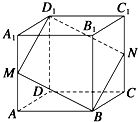 如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )
如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )
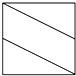
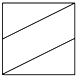
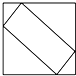
 过抛物线焦点F的直线交抛物线于A、B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
过抛物线焦点F的直线交抛物线于A、B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.