题目内容
设a,b,c∈R,a2+(b+1)2+c2=3,则a+b+c的最小值是 .
考点:基本不等式
专题:不等式的解法及应用
分析:(法一)利用柯西不等式(a+b+c)2=(a•1+b•1+c•1)2≤(a2+b2+c2)(12+12+12),即可求解;
(法二)直接利用基本不等式,即可求解.
(法二)直接利用基本不等式,即可求解.
解答:
解:(法一)由柯西不等式:
[a2+(b+1)2+c2](12+12+12)≥[a+(b+1)+c]2=(a+b+c+1)2,
所以(a+b+c+1)2≤9,
解得-4≤a+b+c≤2,
所以最小值为-4.
(法二)令b+1=t,则a2+t2+c2=1,
∵a2+t2≥2at,t2+c2≥2tc,a2+c2≥2ac
∴(a+t+c)2=a2+t2+c2+2at+2tc+2ac≤a2+t2+c2+(a2+t2)+(t2+c2)+(a2+c2)=3(a2+t2+c2)
∵a2+t2+c2=3,
∴(a+t+c)2≤9,即(a+b+1+c)2≤9
∴-3≤a+b+c+1≤3,
∴-4≤a+b+c+1≤2,
则a+b+c的最小值是-4.
故答案为:-4.
[a2+(b+1)2+c2](12+12+12)≥[a+(b+1)+c]2=(a+b+c+1)2,
所以(a+b+c+1)2≤9,
解得-4≤a+b+c≤2,
所以最小值为-4.
(法二)令b+1=t,则a2+t2+c2=1,
∵a2+t2≥2at,t2+c2≥2tc,a2+c2≥2ac
∴(a+t+c)2=a2+t2+c2+2at+2tc+2ac≤a2+t2+c2+(a2+t2)+(t2+c2)+(a2+c2)=3(a2+t2+c2)
∵a2+t2+c2=3,
∴(a+t+c)2≤9,即(a+b+1+c)2≤9
∴-3≤a+b+c+1≤3,
∴-4≤a+b+c+1≤2,
则a+b+c的最小值是-4.
故答案为:-4.
点评:本题主要考查一般形式的柯西不等式的应用,掌握柯西不等式(a2+b2+c2)(x2+y2+z2)≥(ax+by+cz)2是关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
在等差数列{an}中,a4=2-a3,则此数列{an}的前6项和为( )
| A、12 | B、3 | C、36 | D、6 |
在△ABC中,一定成立的等式是( )
| A、asinB=bsinA |
| B、acosB=bcosA |
| C、atanB=btanA |
| D、asinA=bsinB |
 已知梯形ABCD,AD∥BC,∠ABC=∠BAD=
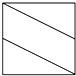
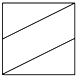
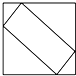
已知梯形ABCD,AD∥BC,∠ABC=∠BAD=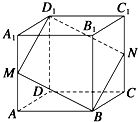 如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )
如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )