题目内容
设函数f(x)=x(ex+ae-x)(x∈R)是偶函数,二项式(x-
)6的展开式中,x2项的系数为 .
| 2a |
| x |
考点:二项式系数的性质
专题:计算题,二项式定理
分析:由函数是偶函数,直接用特殊值求解a,(x-
)6的通项为Tr+1=C6r•(x)6-r•(
)r=C6r•2r•(x)6-2r,令6-2r=2,可得r=2,将r=2代入通项可得T3=60x2,即可得答案.
| 2a |
| x |
| 2 |
| x |
解答:
解:因为函数f(x)=x(ex+ae-x)(x∈R)是偶函数,
所以g(x)=ex+ae-x为奇函数
由g(0)=0,得a=-1.
根据二项式定理,(x-
)6的通项为Tr+1=C6r•(x)6-r•(
)r=C6r•2r•(x)6-2r,
当6-2r=2时,即r=2时,可得T3=60x2,
即x2项的系数为60,
故答案为:60.
所以g(x)=ex+ae-x为奇函数
由g(0)=0,得a=-1.
根据二项式定理,(x-
| 2a |
| x |
| 2 |
| x |
当6-2r=2时,即r=2时,可得T3=60x2,
即x2项的系数为60,
故答案为:60.
点评:本题考查二项式定理的运用,注意二项式系数与某一项的系数的区别.

练习册系列答案
相关题目
已知函数f(x)=
,若|f(x)|≥a(x-1),则a的取值范围是( )
|
| A、(-∞,-1] |
| B、(-∞,1] |
| C、[-1,1] |
| D、[-1,0] |
不等式|x+2a|+|x-a|≥3对任意实数x都成立,则实数a的取值范围是( )
| A、(-∞,-3]∪[3,+∞) |
| B、(-∞,-1]∪[1,+∞) |
| C、[-3,3] |
| D、[-1,1] |
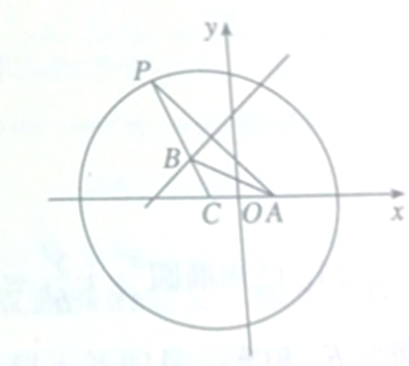 如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.
如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.