题目内容
直角坐标系xoy中,以原点为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=2sinθ,直线l的参数方程为
(t为参数),则圆C截直线l所得的弦长为( )
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:首先把圆的极坐标方程转化成直角坐标方程,进一步把直线的参数方程转化成直角坐标方程,进一步利用直线和圆的位置关系求出所截取的弦长.
解答:
解:已知圆C的极坐标方程为ρ=2sinθ,
则转化成直角坐标方程为:x2+y2=2y
转化成标准方程为:x2+(y-1)2=1,圆心坐标为:(0,1)
直线l的参数方程为
(t为参数),
转化成直角坐标方程为:x-y+1=0
圆C的圆心满足直线的方程.
则:圆C截直线l所得的弦长2.
故选:C
则转化成直角坐标方程为:x2+y2=2y
转化成标准方程为:x2+(y-1)2=1,圆心坐标为:(0,1)
直线l的参数方程为
|
转化成直角坐标方程为:x-y+1=0
圆C的圆心满足直线的方程.
则:圆C截直线l所得的弦长2.
故选:C
点评:本题考查的知识要点:圆的极坐标方程与直角坐标方程的互化,直线的参数方程和直角坐标方程的互化,判断直线和曲线的位置关系.属于基础题型.

练习册系列答案
相关题目
给出函数①y=x3cosx,②y=sin2x,③y=|x2-x|,④y=ex-e-x,其中是奇函数的是( )
| A、①② | B、①④ | C、②④ | D、③④ |
设函数f(x)=
在[-2,2]上的最大值为2,则a的取值范围是( )
|
A、(-∞,
| ||
B、[
| ||
| C、(-∞,0) | ||
D、[0,
|
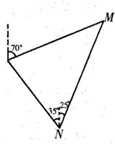 如图,一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行,灯塔M原来在轮船的北偏东25°方向上,经过30分钟后,灯塔在轮船的北偏东70°方向上,则灯塔M距离N处的海里数为( )
如图,一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行,灯塔M原来在轮船的北偏东25°方向上,经过30分钟后,灯塔在轮船的北偏东70°方向上,则灯塔M距离N处的海里数为( )A、
| ||||
B、
| ||||
C、30(
| ||||
D、30(
|
已知两点A(-2,-4),B(1,5)到直线l:ax+y+1=0的距离相等,则实数a的值为( )
| A、-3 | B、3 |
| C、-3或3 | D、1或3 |