题目内容
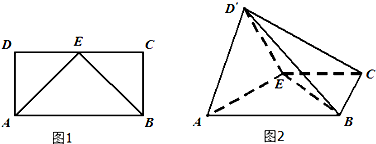
如图1,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE(如图2).
(1)求证:AD′⊥BE
(2)求四棱锥D′-ABCE的体积;
(3)在棱D′E上是否存在一点P,使得D′B∥平面PAC,若存在,求出点P的位置,不存在,说明理由.
(1)求证:AD′⊥BE
(2)求四棱锥D′-ABCE的体积;
(3)在棱D′E上是否存在一点P,使得D′B∥平面PAC,若存在,求出点P的位置,不存在,说明理由.

考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)证明BE⊥AE,然后BE⊥平面D'AE,通过直线与平面垂直的性质定理证明AD'⊥BE.
(2)取AE中点F,连接D'F,证明D'F⊥平面ABCE,得到棱锥的高,然后求解棱锥的体积.
(3)连接AC交BE于Q,连接PQ,证明D'B∥PQ利用比例关系,即可在棱D'E上存在一点P,且EP=
ED′,使得D'B∥平面PAC.
(2)取AE中点F,连接D'F,证明D'F⊥平面ABCE,得到棱锥的高,然后求解棱锥的体积.
(3)连接AC交BE于Q,连接PQ,证明D'B∥PQ利用比例关系,即可在棱D'E上存在一点P,且EP=
| 1 |
| 3 |
解答:
解: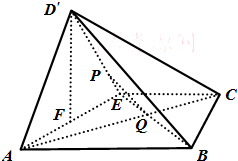 (1)证明:在长方形ABCD中,△DAE和△CBE为等腰直角三角形,
(1)证明:在长方形ABCD中,△DAE和△CBE为等腰直角三角形,
∴∠DEA=∠CEB=45°,∴∠AEB=90°,即BE⊥AE…(2分)
∵平面D'AE⊥平面ABCE,且平面D'AE∩平面ABCE=AE,
∴BE⊥平面D'AE,AD'?平面D'AE
∴AD'⊥BE…(4分)
(2)取AE中点F,连接D'F,则D'F⊥AE
∵平面D'AE⊥平面ABCE,
且平面D'AE∩平面ABCE=AE,D'F⊥平面ABCE,
∴VD′-ABCE=
SABCE•D′F=
•
•(1+2)•1•
=
…(8分)
(3)解:如图,连接AC交BE于Q,连接PQ,
若D'B∥平面PAC
∵D'B?平面D'BE
平面D'BE∩平面PAC=PQ
∴D'B∥PQ…(10分)
∴在△EBD'中,
=
,∵在梯形ABCE中
=
=
∴
=
=
,即EP=
ED′
∴在棱D'E上存在一点P,且EP=
ED′,使得D'B∥平面PAC…(12分)
 (1)证明:在长方形ABCD中,△DAE和△CBE为等腰直角三角形,
(1)证明:在长方形ABCD中,△DAE和△CBE为等腰直角三角形,∴∠DEA=∠CEB=45°,∴∠AEB=90°,即BE⊥AE…(2分)
∵平面D'AE⊥平面ABCE,且平面D'AE∩平面ABCE=AE,
∴BE⊥平面D'AE,AD'?平面D'AE
∴AD'⊥BE…(4分)
(2)取AE中点F,连接D'F,则D'F⊥AE
∵平面D'AE⊥平面ABCE,
且平面D'AE∩平面ABCE=AE,D'F⊥平面ABCE,
∴VD′-ABCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
(3)解:如图,连接AC交BE于Q,连接PQ,
若D'B∥平面PAC
∵D'B?平面D'BE
平面D'BE∩平面PAC=PQ
∴D'B∥PQ…(10分)
∴在△EBD'中,
| EP |
| PD′ |
| EQ |
| QB |
| EQ |
| QB |
| EC |
| AB |
| 1 |
| 2 |
∴
| EP |
| PD′ |
| EQ |
| QB |
| 1 |
| 2 |
| 1 |
| 3 |
∴在棱D'E上存在一点P,且EP=
| 1 |
| 3 |
点评:本题考查几何体的体积的求法,直线与平面垂直的性质定理的应用,直线与平面平行的判断,考查空间想象能力以及计算能力.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知p:x2-6x-27≤0,q:|x-1|≤m(m>0),若q是p的必要而不充分条件,则实数m的取值范围是( )
| A、m≤4 | B、m<4 |
| C、m≥8 | D、m>8 |
化简cos(45°-α)cos(α+15°)-sin(45°-α)sin(α+15°)的结果是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|