题目内容
12.在△ABC中,内角A,B,C的对边分别为a,b,c,已知acos2$\frac{C}{2}$+ccos2$\frac{A}{2}$=$\frac{3}{2}$b.(1)求证a,b,c成等差数列;
(2)若b=2,当角B取最大值时,求△ABC面积S.
分析 (1)已知等式利用正弦定理化简,再利用二倍角的余弦函数公式及两角和与差的正弦函数公式变形,整理后再利用正弦定理化简,利用等差数列的性质判断即可得证;
(2)利用基本不等式和余弦定理求出sinB的最大值和ac的值,代入面积公式计算.
解答 (1)证明:∵acos2$\frac{C}{2}$+ccos2$\frac{A}{2}$=$\frac{3}{2}$b,
∴a×$\frac{1+cosC}{2}$+c×$\frac{1+cosA}{2}$=$\frac{3b}{2}$.
∴sinA(1+cosC)+sinC(1+cosA)=3sinB.
即sinA+sinC+sinAcosC+sinCcosA=3sinB.
∵sinAcosC+sinCcosA=sin(A+C)=sinB.
∴sinA+sinC=2sinB.
∴a+c=2b.
∴a,b,c成等差数列.
(2)解:a+c=2b=4,∴a2+c2=16-2ac,∴ac≤($\frac{a+c}{2}$)2=4.
∵cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{12-2ac}{2ac}$=$\frac{6}{ac}-1$,
∴当ac=4时cosB取得最小值$\frac{1}{2}$,即B取得最大值,此时sinB=$\frac{\sqrt{3}}{2}$.
∴S=$\frac{1}{2}$acsinB=$\frac{1}{2}×4×\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
点评 本题考查了三角函数的恒等变换,正余弦定理的应用,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
2.已知向量$\overrightarrow{m}$=(1,2),$\overrightarrow{n}$=(a,-1),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则实数a的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
3.在公差不为0的等差数列{an}中,a2+a4=ap+aq,记$\frac{1}{p}$+$\frac{9}{q}$的最小值为m,若数列{bn}满足b1=$\frac{2}{11}$m,2bn+1-bn•bn+1=1,则b1+$\frac{{b}_{2}}{{2}^{2}}$+$\frac{{b}_{3}}{{3}^{2}}$+…+$\frac{{b}_{100}}{10{0}^{2}}$=( )
| A. | $\frac{97}{100}$ | B. | $\frac{99}{100}$ | C. | $\frac{100}{101}$ | D. | $\frac{102}{101}$ |
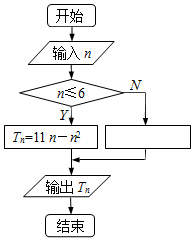 已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.
已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.