题目内容
4.求过点P(2,2)且与圆x2+y2-2x=0相切的直线方程.分析 由题意易得圆心和半径,分类讨论结合待定系数可得.
解答 解:圆x2+y2-2x=0可化为(x-1)2+y2=1,故圆的圆心为(1,0),半径为1,
当过点P(2,2)的直线无斜率时,满足与圆相切,此时方程为x=2;
当直线有斜率时,设直线方程为y-2=k(x-2),即kx-y+2-2k=0,
由直线和圆相切可得圆心到直线的距离等于半径,即$\frac{|k+2-2k|}{\sqrt{{k}^{2}+1}}$=1,
解得k=$\frac{3}{4}$,故直线方程为y-2=$\frac{3}{4}$(x-2),即3x-4y+2=0
综上可得切线方程为x=2或3x-4y+2=0
点评 本题考查圆的切线问题,涉及点到直线的距离公式和分类讨论的思想,属中档题.

练习册系列答案
相关题目
14.下列函数既是偶函数,又在(0,π)上单调递增的是( )
| A. | y=|sinx| | B. | y=tan|x| | C. | y=cosx | D. | y=-cosx |
15.sin50°cos20°-sin40°cos70°等于( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
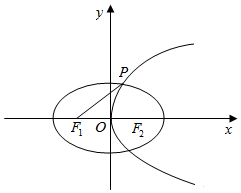 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.