题目内容
2.已知向量$\overrightarrow{m}$=(1,2),$\overrightarrow{n}$=(a,-1),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则实数a的值为( )| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 直接利用向量垂直数量积为0列式求得a值.
解答 解:∵$\overrightarrow{m}$=(1,2),$\overrightarrow{n}$=(a,-1),
∴由$\overrightarrow{m}$⊥$\overrightarrow{n}$,得1×a+2×(-1)=0,
即a=2.
故选:D.
点评 本题考查数量积判断两个向量的垂直关系,考查数量积的坐标运算,是基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
17.设Sn为数列{an}的前n项的和,且${S_n}=\frac{3}{2}({a_n}-1)(n∈{{N}^*})$,则an=( )
| A. | 3(3n-2n) | B. | 3n+2n | C. | 3n | D. | 3•2n-1 |
14.下列函数既是偶函数,又在(0,π)上单调递增的是( )
| A. | y=|sinx| | B. | y=tan|x| | C. | y=cosx | D. | y=-cosx |
11.若z•(1+i)=2-i(i为虚数单位),则复数z的虚数部分为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$i | D. | -$\frac{3}{2}$i |
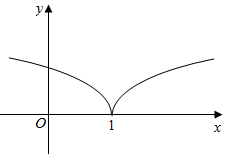 如果函数y=f(x)的定义域为R,并且大致图象如图所示,那么函数的解析式可以是f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{ln(2-x),x<1}\end{array}\right.$(只需写出一个正确答案)
如果函数y=f(x)的定义域为R,并且大致图象如图所示,那么函数的解析式可以是f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{ln(2-x),x<1}\end{array}\right.$(只需写出一个正确答案)