题目内容
17.在△ABC中,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3$\overrightarrow{BA}$•$\overrightarrow{BC}$,则$\frac{tanA}{tanB}$=$\frac{1}{3}$.分析 可画出图形,然后分别过A,B作BC,AC的垂线AD,BE,垂足分别为D,E,根据三角形的面积公式便可得到:$|\overrightarrow{AB}||\overrightarrow{AC}|=|\overrightarrow{BA}||\overrightarrow{BC}|•\frac{sinB}{sinA}$,而由条件$\overrightarrow{AB}•\overrightarrow{AC}=3\overrightarrow{BA}•\overrightarrow{BC}$便可得到$|\overrightarrow{AB}||\overrightarrow{AC}|cosA=3|\overrightarrow{BA}||\overrightarrow{BC}|cosB$,带入前面的式子即可得到$\frac{sinB}{sinA}•cosA=3cosB$,这样即可求出$\frac{tanA}{tanB}$的值.
解答 解:如图,过A作AD⊥BC,垂足为D,作BE⊥AC,垂足为E,则: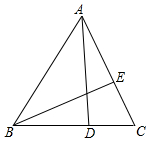
$|\overrightarrow{AB}|sinA•|\overrightarrow{AC}|=|\overrightarrow{BA}|sinB•|\overrightarrow{BC}|$;
∴$|\overrightarrow{AB}||\overrightarrow{AC}|=|\overrightarrow{BA}||\overrightarrow{BC}|•\frac{sinB}{sinA}$;
由$\overrightarrow{AB}•\overrightarrow{AC}=3\overrightarrow{BA}•\overrightarrow{BC}$得,$|\overrightarrow{AB}||\overrightarrow{AC}|cosA=3|\overrightarrow{BA}||\overrightarrow{BC}|cosB$;
∴$|\overrightarrow{BA}||\overrightarrow{BC}|•\frac{sinB}{sinA}•cosA=3|\overrightarrow{BA}||\overrightarrow{BC}|cosB$;
∴$\frac{sinB}{sinA}•cosA=3cosB$;
∴$\frac{sinB}{cosB}=3•\frac{sinA}{cosA}$,即tanB=3tanA;
∴$\frac{tanA}{tanB}=\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 考查正弦函数的定义,三角形的面积公式,以及数量积的计算公式,弦化切公式.

 考前必练系列答案
考前必练系列答案| A. | 3 | B. | 6 | C. | $6\sqrt{2}$ | D. | 2 |
| 学生 | A | B | C | D | E |
| 数学(x分) | 89 | 91 | 93 | 95 | 97 |
| 物理(y分) | 87 | 89 | 89 | 92 | 93 |
(2)试估计某同学数学考100分时,他的物理得分;
(3)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以X表示选中的同学中物理成绩高于90分的人数,试解决下列问题:
①求至少选中1名物理成绩在90分以下的同学的概率;
②求随机变变量X的分布列及数学期望E(X).
(附:回归方程::$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$)
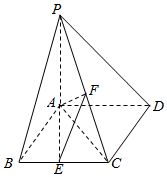 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.