题目内容
20.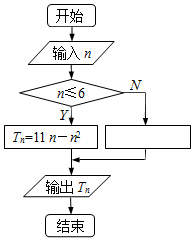 已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.
已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.
分析 首先对a1=10.a2=8,a3=6时,分别求前6项之和,和6项之后的和.通过等差数列求和公式,分别求出之后合并,即可解出Tn的值即可得解.
解答 解:当a1=10.a2=8,a3=6时,
an=-2n+12,sn=$\frac{n(10+12-2n)}{2}$=-n2+11n,s6=30,
当n≤6时,an≥0,当n>6时,an<0
∴当n>6时
Tn=|a1|+|a2|+…+|a5|+|a6|+…+|an|
=a1+a2+…+a5+a6-a7…-an
=a1+a2+…+a5+a6-(a7…+an)
=S6-(Sn-S6)
=n2-11n+60
故答案为:Tn=n2-11n+60.
点评 本题考查程序框图,而实际考查等差数列求和公式的熟练运用.属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
11.若z•(1+i)=2-i(i为虚数单位),则复数z的虚数部分为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$i | D. | -$\frac{3}{2}$i |
15.sin50°cos20°-sin40°cos70°等于( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
5.焦点在x轴上的椭圆$\frac{x^2}{3n}+{y^2}=1(n>0)$的焦距为$4\sqrt{2}$,则长轴长是( )
| A. | 3 | B. | 6 | C. | $6\sqrt{2}$ | D. | 2 |
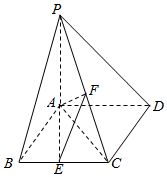 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.