题目内容

1．曲线f（x）=x2上两点A（2，4）和B（2+d，f（2+d））），作割线，当d=0.1时，割线的斜率是（　　）
A．4B．4.1C．4.2D．4.3

分析 利用已知条件求出B的坐标，然后求解割线的斜率．

解答 解：曲线f（x）=x2上两点A（2，4）和B（2+d，f（2+d））），作割线，当d=0.1时，
可得B（2.1，2.12），
割线的斜率是：$\frac{{2.1}^{2}-4}{2.1-2}$=4.1．
故选：B．

点评 本题考查抛物线的应用，直线与抛物线的位置关系，直线的斜率的求法，是基础题．

练习册系列答案
相关题目
17．已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是$\left\{\begin{array}{l}{x=t}\\{y=t-a}\end{array}\right.$（t为参数）．
（Ⅰ）求曲线C的直角坐标方程和直线l的普通方程；
（Ⅱ）设点P（0，-a），若直线l与曲线C交于A，B两点，且|PA||PB|=2，求实数a的值．
18．等差数列{an}的前n项和为Sn，若a1=20，S10=S15，则当n=12或13时，Sn取最大值．
9．设数列{an}的前n项和为Sn，满足${a_n}+{S_n}=A{n^2}+Bn+C$（A≠0，n∈N*）．
（1）当C=1时，
①设bn=an-n，若${a_1}=\frac{3}{2}$，${a_2}=\frac{9}{4}$．求实数A，B的值，并判定数列{bn}是否为等比数列；
②若数列{an}是等差数列，求$\frac{B-1}{A}$的值；
（2）当C=0时，若数列{an}是等差数列，a1=1，且?n∈N*，$λ-\frac{3}{n+1}≤\sum_{i=1}^n{\sqrt{1+\frac{1}{a_i^2}+\frac{1}{{a_{i+1}^2}}}}$，求实数λ的取值范围．
16．在三棱锥P-ABC中，底面△ABC为正三角形，且PA=PB=PC，G为△PAC的重心，过G作三棱锥的一个截面，使截面平行于直线AC与PB，若截面是边长为2的正方形，则三棱锥的体积为（　　）
A．$\frac{3\sqrt{3}}{3}$B．$\frac{9\sqrt{11}}{4}$C．$\frac{16\sqrt{2}}{3}$D．18$\sqrt{2}$
6．如图程序运行的结果是96．
13．设P为直线3x+4y+3=0上的动点，过点P做圆C：x2+y2-2x-2y+1=0的两条切线，切点分别为A，B，当四边形PACB的面积最小时，∠APB=$\frac{π}{3}$．
10．已知Sn为等差数列{an}的前n项和，a7=10，则S13=130．
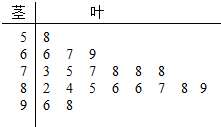11．某上市公司为了解A市用户对其产品的满意度，从该市随机调查了20个用户，得到用户对其产品的满意度评分，并用茎叶图记录分数如图所示．
（Ⅰ）根据样本数据估计A市用户对产品的满意度评分的平均值；
（Ⅱ）根据用户满意度评分，若评分在70分以上（含70分），用户对产品满意，根据所给数据，以事件发生的频率作为相应事件发生的概率，若从A市随机抽取3个用户，记X表示对产品满意的用户个数，求X的分布列及均值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网