题目内容
10.已知Sn为等差数列{an}的前n项和,a7=10,则S13=130.分析 由题意和等差数列的性质以及求和公式可得.
解答 解:由题意和等差数列的性质可得a1+a13=2a7=20,
∴由等差数列的求和公式可得S13=$\frac{13({a}_{1}+{a}_{13})}{2}$=$\frac{13×20}{2}$=130
故答案为:130
点评 本题考查等差数列的性质和求和公式,属基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
1.曲线f(x)=x2上两点A(2,4)和B(2+d,f(2+d))),作割线,当d=0.1时,割线的斜率是( )
| A. | 4 | B. | 4.1 | C. | 4.2 | D. | 4.3 |
18.下列函数中既是奇函数又在区间,[-1,1]上单调递减的是( )
| A. | y=sinx | B. | y=-|x+1| | C. | $y=ln\frac{2-x}{2+x}$ | D. | y=$\frac{1}{2}$(2x+2-x) |
19.已知集合A={x|(x-1)(x+2)<0},B={x|-3<x<0},则A∩B=( )
| A. | (-∞,-2) | B. | (-2,0) | C. | (0,1) | D. | (1,+∞) |
20.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程为$y=\frac{3}{4}x$,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{5}$ |
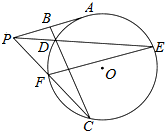 如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证: