题目内容
16.在三棱锥P-ABC中,底面△ABC为正三角形,且PA=PB=PC,G为△PAC的重心,过G作三棱锥的一个截面,使截面平行于直线AC与PB,若截面是边长为2的正方形,则三棱锥的体积为( )| A. | $\frac{3\sqrt{3}}{3}$ | B. | $\frac{9\sqrt{11}}{4}$ | C. | $\frac{16\sqrt{2}}{3}$ | D. | 18$\sqrt{2}$ |
分析 作出符合条件的截面,根据比例线段得出三棱锥的底面边长和侧棱长,求出棱锥的高,代入体积公式计算.
解答 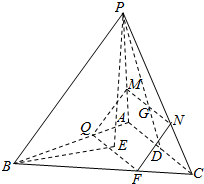 解:取AC中点D,连结AD,过G作MN∥AC,交PA于M,交PC于N,过M作MQ∥PB交AB于Q,过N作NF∥PB交BC于F.
解:取AC中点D,连结AD,过G作MN∥AC,交PA于M,交PC于N,过M作MQ∥PB交AB于Q,过N作NF∥PB交BC于F.
则四边形MNFQ为符合条件的截面.
∵G是△PAC的重心,∴$\frac{PN}{PC}$=$\frac{MN}{AC}=\frac{PG}{PD}=\frac{2}{3}$,∴AC=3.$\frac{CN}{CP}=\frac{1}{3}$.
∵NF∥PB,∴$\frac{NF}{PB}=\frac{CN}{PC}$=$\frac{1}{3}$,∴PB=6.
过P作PE⊥平面ABC,垂足为E,∵△ABC为正三角形,∴E是△ABC的中心.
∴BE=$\sqrt{3}$.∴PE=$\sqrt{P{B}^{2}-B{E}^{2}}$=$\sqrt{33}$.
∴V棱锥P-ABC=$\frac{1}{3}$S△ABC•PE=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{3}^{2}×\sqrt{33}$=$\frac{9\sqrt{11}}{4}$.
故选:B.
点评 本题考察了棱锥的结构特征,线面平行的性质,相似三角形及体积计算,作出棱锥的截面是解题关键,属于中档题.

练习册系列答案
相关题目
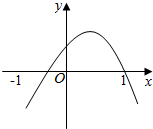
1.曲线f(x)=x2上两点A(2,4)和B(2+d,f(2+d))),作割线,当d=0.1时,割线的斜率是( )
| A. | 4 | B. | 4.1 | C. | 4.2 | D. | 4.3 |
6.设单位向量$\overrightarrow{e_1}$、$\overrightarrow{e_2}$对于任意实数λ都有|$\overrightarrow{e_1}$+$\frac{1}{2}$$\overrightarrow{e_2}$|≤|$\overrightarrow{e_1}$-λ$\overrightarrow{e_2}$|成立,则向量$\overrightarrow{e_1}$、$\overrightarrow{e_2}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直.AB=$\sqrt{2}$,AF=1.M是线段EF的中点
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直.AB=$\sqrt{2}$,AF=1.M是线段EF的中点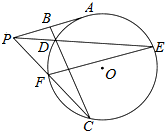 如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证: