题目内容
 函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交与点P、Q,点N(1,0),若△PQN的面积为S时点M恰好有两个,则S的取值范围为( )
函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交与点P、Q,点N(1,0),若△PQN的面积为S时点M恰好有两个,则S的取值范围为( )A、[
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:设M(t,t2),利用导数求出函数在M点处的切线方程,求出P,Q点的坐标,由三角形的面积公式求出△PQN的面积,由面积等于S整理,得到t3-4t2+4t=4S,令g(t)=t3-4t2+4t,由导数求出g(t)的最大值,再求出g(0),g(1)的值,从而得到△PQN的面积为S时点M恰好有两个时的4S的范围,则S的范围可求.
解答:
解:设点M(t,t2),
由f(x)=x2(0<x<1),得:f′(x)=2x,
∴过点M的切线PQ的斜率k=2t.
∴切线PQ的方程为y=2tx-t2.
取y=0,得x=
,
取x=1,得y=2t-t2,
∴P(
,0)、Q(1,2t-t2),
∴S△PQN=
(1-
)(2t-t2)=S.
整理得:t3-4t2+4t-4S=0.
即t3-4t2+4t=4S.
令g(t)=t3-4t2+4t,
则g′(t)=3t2-8t+4,
由g′(t)=0,解得t1=
,t2=2(舍).
∴当t∈(0,
)时,g′(t)>0,g(t)为增函数.
当t∈(
,1)时,g′(t)<0,g(t)为减函数.
∴当t=
时,g(t)有极大值,也就是(0,1)上的最大值为
.
又g(0)=0,g(1)=1.
∴要使△PQN的面积为S时点M恰好有两个,
则1<4S<
,即
<S<
.
∴S的取值范围为(
,
).
故选:C.
由f(x)=x2(0<x<1),得:f′(x)=2x,
∴过点M的切线PQ的斜率k=2t.
∴切线PQ的方程为y=2tx-t2.
取y=0,得x=
| t |
| 2 |
取x=1,得y=2t-t2,
∴P(
| t |
| 2 |
∴S△PQN=
| 1 |
| 2 |
| t |
| 2 |
整理得:t3-4t2+4t-4S=0.
即t3-4t2+4t=4S.
令g(t)=t3-4t2+4t,
则g′(t)=3t2-8t+4,
由g′(t)=0,解得t1=
| 2 |
| 3 |
∴当t∈(0,
| 2 |
| 3 |
当t∈(
| 2 |
| 3 |
∴当t=
| 2 |
| 3 |
| 32 |
| 27 |
又g(0)=0,g(1)=1.
∴要使△PQN的面积为S时点M恰好有两个,
则1<4S<
| 32 |
| 27 |
| 1 |
| 4 |
| 8 |
| 27 |
∴S的取值范围为(
| 1 |
| 4 |
| 8 |
| 27 |
故选:C.
点评:本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数求函数的最值,考查了数学转化思想方法,训练了分离变量法,是中档题.

练习册系列答案
相关题目
二次不等式ax2+bx+1>0的解集为{x|-1<x<
},则ab的值为( )
| 1 |
| 3 |
| A、-5 | B、5 | C、-6 | D、6 |
双曲线
-
=1的左、右焦点为F1,F2,直线x=
与双曲线的渐近线交于点P,过点P且与x轴平行的直线交双曲线右支于点M,过点M做x轴的垂线,垂足为N,若
=3
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| 2 |
| F1N |
| NF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知直线mx+(1-n)y+1=0(m>0,n>0)和直线x+2y+1=0平行,则
+
的最小值是( )
| 1 |
| m |
| 1 |
| n |
A、2
| ||
B、3+2
| ||
C、4
| ||
D、3+
|
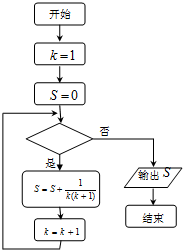
如果执行如图的程序框图,那么输出的S=
,那么判断框内是( )
| 2013 |
| 2014 |

| A、k≤2013? |
| B、k≤2014? |
| C、k≥2013? |
| D、k≥2014? |
函数f(x)=xsinx在区间[0,4]上的零点个数( )
| A、0 | B、1 | C、2 | D、3 |
 如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.
如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.