题目内容
从1,2,3,…,20这20个自然数中,每次任取3个数.
(1)若3个数能组成等差数列,则这样的等差数列共有 个;若组成等比数列,则这样的等比数列共有 个;
(2)若3个数的和是3的倍数,则这样的数组有 个;若其和是大于10的偶数,则这样的数组有 个;
(3)若所取3个数中每2个数之间至少相隔2个自然数,则这样的数组有 个.
(1)若3个数能组成等差数列,则这样的等差数列共有
(2)若3个数的和是3的倍数,则这样的数组有
(3)若所取3个数中每2个数之间至少相隔2个自然数,则这样的数组有
考点:等差数列的性质,等比数列的性质
专题:排列组合
分析:(1)采用分类计数原理和组合数的意义即可求解;
(2)将20个数分为3组,3的倍数,3的倍数加1,3的倍数加2,分类计数即可确定3个数的和是3的倍数的数组;
(3)建立22个小球模型,采用捆绑插空法即可解决.
(2)将20个数分为3组,3的倍数,3的倍数加1,3的倍数加2,分类计数即可确定3个数的和是3的倍数的数组;
(3)建立22个小球模型,采用捆绑插空法即可解决.
解答:
解:(1)设A={1,3,5,…,19},B={2,4,…,20},
从A或B中任取两个数总可作等差数列的第一、二项,且等差中项唯一存在,
∴所求的等差数列共有2(
+
)=180个.
用列举法:公比是3或
的等比数列有4个;
公比是2或
的等比数列有10个;
公比是4或
的等比数列有2个,共有等比数列16个.
(2)设A0={3,6,…,18},A1={1,4,…,19},A2={2,5,…,20},
则从每个集合中任取3个数,或每个集合中各取1个数,
其和必是3的倍数,
故所求的数组共有
+2
+
=384个.
又设A={1,3,5,…,19},B={2,4,…,20},
则从中取3个数且和为偶数的取法有
+
=570种,
其中3个数的和不大于10的有6个.
故符合条件的数组共有570-6=564个.
(3)运用如下模型:将3个黑球与19个白球排成一排,
且每个黑球右边各连排两个白球分别形成一个“位置”,
这样只有13个白球与3个“黑白球组合”排在16个“位置”上,排法有
,
对每种排法中的前20个球从左至右赋值1,2,…,20,
则三个黑球上的数即为取出的数,
∴所取的数组共有
=560个.
故答案为:(1)180,16;(2)384,564;(3)560.
从A或B中任取两个数总可作等差数列的第一、二项,且等差中项唯一存在,
∴所求的等差数列共有2(
| C | 2 10 |
| C | 2 10 |
用列举法:公比是3或
| 1 |
| 3 |
公比是2或
| 1 |
| 2 |
公比是4或
| 1 |
| 4 |
(2)设A0={3,6,…,18},A1={1,4,…,19},A2={2,5,…,20},
则从每个集合中任取3个数,或每个集合中各取1个数,
其和必是3的倍数,
故所求的数组共有
| C | 3 6 |
| C | 3 7 |
| C | 1 6 |
| C | 1 7 |
| C | 1 7 |
又设A={1,3,5,…,19},B={2,4,…,20},
则从中取3个数且和为偶数的取法有
| C | 3 10 |
| C | 1 10 |
| C | 2 10 |
其中3个数的和不大于10的有6个.
故符合条件的数组共有570-6=564个.
(3)运用如下模型:将3个黑球与19个白球排成一排,
且每个黑球右边各连排两个白球分别形成一个“位置”,
这样只有13个白球与3个“黑白球组合”排在16个“位置”上,排法有
| C | 3 16 |
对每种排法中的前20个球从左至右赋值1,2,…,20,
则三个黑球上的数即为取出的数,
∴所取的数组共有
| C | 3 16 |
故答案为:(1)180,16;(2)384,564;(3)560.
点评:本题考查等差数列和等比数列的概念,排列组合的综合应用,解题的关键在能够正确的利用分布计数原理和转化的思想,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
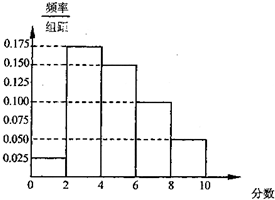 某个团购网站为了更好地满足消费者需求,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是10分.上个月该网站共卖出了100份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.
某个团购网站为了更好地满足消费者需求,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是10分.上个月该网站共卖出了100份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.