题目内容
设Sn为数列an的前n项和，Sn=λan-1，λ为常数，n=1、2、3…
（1）若a3=
，求λ的值
（2）是否存在实数λ，使该数列是等差数列？若存在，求λ的值，若不存在，请说明理由．
（1）若a3=
| a | 2 2 |
（2）是否存在实数λ，使该数列是等差数列？若存在，求λ的值，若不存在，请说明理由．
考点：等差关系的确定,等差数列的性质
专题：等差数列与等比数列
分析：（1）由Sn=λan-1，求出知a1，根据a3=
，即可求出λ的值．
（2）假设存在实数λ，使得数列{an}是等差数列，则2a2=a1+a3，然后解方程，得到矛盾即可得到结论．
| a | 2 2 |
（2）假设存在实数λ，使得数列{an}是等差数列，则2a2=a1+a3，然后解方程，得到矛盾即可得到结论．
解答：
解：（1）∵Sn=λan-1，
∴a1=λa1-1，
a2+a1=λa2-1，
a3+a2+a1=λa3-1，
由a1=λa1-1，得λ≠1，
∴a1=
，a2=
，a3=
，
∵a3=
，
∴
=
，
∴λ=0，或λ=2．
（2）假设存在实数λ，使得数列{an}是等差数列，
则2a2=a1+a3，
由（1）得
=
+
，
∴
=
，
整理得1=0，不成立，
∴不存在实数λ，使得数列{an}是等差数列．
∴a1=λa1-1，
a2+a1=λa2-1，
a3+a2+a1=λa3-1，
由a1=λa1-1，得λ≠1，
∴a1=
| 1 |
| λ-1 |
| λ |
| (λ-1)2 |
| λ2 |
| (λ-1)3 |
∵a3=
| a | 2 2 |
∴
| λ2 |
| (λ-1)3 |
| λ2 |
| (λ-1)4 |
∴λ=0，或λ=2．
（2）假设存在实数λ，使得数列{an}是等差数列，
则2a2=a1+a3，
由（1）得
| 2λ |
| (λ-1)2 |
| 1 |
| λ-1 |
| λ2 |
| (λ-1)3 |
∴
| 2λ |
| (λ-1)2 |
| 2λ2-2λ+1 |
| (λ-1)3 |
整理得1=0，不成立，
∴不存在实数λ，使得数列{an}是等差数列．
点评：点评：本题主要考查等差数列的应用，考查数列的前n项和的求法．解题时要认真审题，考查学生的计算能力．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
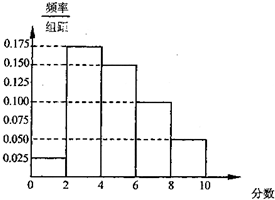某个团购网站为了更好地满足消费者需求，对在其网站发布的团购产品展开了用户调查，每个用户在使用了团购产品后可以对该产品进行打分，最高分是10分．上个月该网站共卖出了100份团购产品，所有用户打分的平均分作为该产品的参考分值，将这些产品按照得分分成以下几组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10]，得到的频率分布直方图如图所示．