题目内容
已知函数f(x)=
,g(x)=
ax2+bx(a≠0)(e为自然对数的底数).
(Ⅰ)若函数f(x)的图象在x=-1处的切线方程为y=
x+n,求m,n的值;
(Ⅱ)若a=-2时,函数h(x)=f(x)-g(x)在(0,+∞)内是增函数,求b的取值范围;
(Ⅲ)当x>0时,设函数f(x)的图象C1与函数g(x)的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
|
| 1 |
| 2 |
(Ⅰ)若函数f(x)的图象在x=-1处的切线方程为y=
| 1 |
| e |
(Ⅱ)若a=-2时,函数h(x)=f(x)-g(x)在(0,+∞)内是增函数,求b的取值范围;
(Ⅲ)当x>0时,设函数f(x)的图象C1与函数g(x)的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:探究型,导数的综合应用
分析:(Ⅰ)先求出f(x)在x<0时的导数,从而得到在x=-1处的切线斜率,并求出切点,根据切点在切线上,得到一方程,及切线斜率为e-1,得到另一个方程,求出m,n;
(Ⅱ)首先化简a=-2时的函数h(x),根据函数h(x)在(0,+∞)内是增函数等价为h'(x)≥0在(0,+∞)内恒成立,通过分离参数,求出
+2x(x>0)的最小值2
,令b不大于2
;
(Ⅲ)假设C1在点M处的切线与C2在点N处的切线平行,设出P,Q的坐标,求出中点R的横坐标,分别求出C1在点M处的切线斜率k1与C2在点N处的切线斜率k2,令k1=k2,两边同时乘以x2-x1,整理得到∴ln
=
,构造函数r(t)=lnt-
(t>1),应用导数说明r(t)在t>1上单调递增,从而r(t)>r(1),即lnt>
,显然矛盾,故假设不成立,即不存在.
(Ⅱ)首先化简a=-2时的函数h(x),根据函数h(x)在(0,+∞)内是增函数等价为h'(x)≥0在(0,+∞)内恒成立,通过分离参数,求出
| 1 |
| x |
| 2 |
| 2 |
(Ⅲ)假设C1在点M处的切线与C2在点N处的切线平行,设出P,Q的坐标,求出中点R的横坐标,分别求出C1在点M处的切线斜率k1与C2在点N处的切线斜率k2,令k1=k2,两边同时乘以x2-x1,整理得到∴ln
| x2 |
| x1 |
2(
| ||
|
| 2(t-1) |
| t+1 |
| 2(t-1) |
| t+1 |
解答:
解:(Ⅰ)当x<0时,f(x)=ex-
x2+mx,导数f'(x)=ex-x+m,
∴f'(-1)=e-1+1+m,
即函数f(x)的图象在x=-1处的切线斜率为e-1+1+m,
切点为(-1,e-1-
-m),
∵函数f(x)的图象在x=-1处的切线方程为y=
x+n,
∴e-1+1+m=
,-
+n=e-1-
-m,
∴m=-1,n=
+
;
(Ⅱ)a=-2时,函数h(x)=f(x)-g(x)在(0,+∞)的解析式是h(x)=lnx+x2-bx,
导数h'(x)=
+2x-b,
∵函数h(x)在(0,+∞)内是增函数,
∴h'(x)≥0即
+2x-b≥0在(0,+∞)内恒成立,
∴b≤(
+2x)min,
∵x>0时,
+2x≥2
=2
,
∴b≤2
,
故b的取值范围是(-∞,2
];
(Ⅲ)假设C1在点M处的切线与C2在点N处的切线平行,
设点P(x1,y1),Q(x2,y2),0<x1<x2,
则由题意得点M、N的横坐标与中点R的横坐标相等,
且为x0=
,
∵x>0时,f'(x)=
,g'(x)=ax+b,
∴C1在点M处的切线斜率为k1=
=
,
C2在点N处的切线斜率为k2=ax0+b=
+b,
由于两切线平行,则k1=k2,
即
=
+b,则两边同乘以(x2-x1),得
=
(x22-x12)+b(x2-x1)
=(
x22+bx2)-(
x12+bx1)=y2-y1=lnx2-lnx1,
∴ln
=
,
设t=
,则lnt=
,t>1①,
令r(t)=lnt-
,t>1,
则r'(t)=
-
=
,
∵t>1,r'(t)>0,
∴r(t)在(1,+∞)上单调递增,
∴r(t)>r(1)=0,
∴lnt>
,
这与①矛盾,假设不成立,
故C1在点M处的切线与C2在点N处的切线不平行.
| 1 |
| 2 |
∴f'(-1)=e-1+1+m,
即函数f(x)的图象在x=-1处的切线斜率为e-1+1+m,
切点为(-1,e-1-
| 1 |
| 2 |
∵函数f(x)的图象在x=-1处的切线方程为y=
| 1 |
| e |
∴e-1+1+m=
| 1 |
| e |
| 1 |
| e |
| 1 |
| 2 |
∴m=-1,n=
| 2 |
| e |
| 1 |
| 2 |
(Ⅱ)a=-2时,函数h(x)=f(x)-g(x)在(0,+∞)的解析式是h(x)=lnx+x2-bx,
导数h'(x)=
| 1 |
| x |
∵函数h(x)在(0,+∞)内是增函数,
∴h'(x)≥0即
| 1 |
| x |
∴b≤(
| 1 |
| x |
∵x>0时,
| 1 |
| x |
|
| 2 |
∴b≤2
| 2 |
故b的取值范围是(-∞,2
| 2 |
(Ⅲ)假设C1在点M处的切线与C2在点N处的切线平行,
设点P(x1,y1),Q(x2,y2),0<x1<x2,
则由题意得点M、N的横坐标与中点R的横坐标相等,
且为x0=
| x1+x2 |
| 2 |
∵x>0时,f'(x)=
| 1 |
| x |
∴C1在点M处的切线斜率为k1=
| 1 |
| x0 |
| 2 |
| x1+x2 |
C2在点N处的切线斜率为k2=ax0+b=
| a(x1+x2) |
| 2 |
由于两切线平行,则k1=k2,
即
| 2 |
| x1+x2 |
| a(x1+x2) |
| 2 |
| 2(x2-x1) |
| x2+x1 |
| a |
| 2 |
=(
| a |
| 2 |
| a |
| 2 |
∴ln
| x2 |
| x1 |
2(
| ||
|
设t=
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
令r(t)=lnt-
| 2(t-1) |
| t+1 |
则r'(t)=
| 1 |
| t |
| 4 |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
∵t>1,r'(t)>0,
∴r(t)在(1,+∞)上单调递增,
∴r(t)>r(1)=0,
∴lnt>
| 2(t-1) |
| t+1 |
这与①矛盾,假设不成立,
故C1在点M处的切线与C2在点N处的切线不平行.
点评:本题主要考查导数在函数中的综合应用:解决切线问题,判断单调性及应用.考查探究性问题,构造函数通过求导应用单调性解决,考查灵活将式子变形的能力,有一定的难度.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
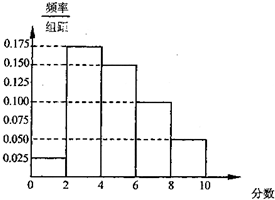 某个团购网站为了更好地满足消费者需求,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是10分.上个月该网站共卖出了100份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.
某个团购网站为了更好地满足消费者需求,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是10分.上个月该网站共卖出了100份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.