题目内容
下列命题中:
①若p、q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件;
②若p为:存在x∈R,x2+2x+2≤0,则p为:任意x∈R,x2+2x+2>0;
③已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q成立的必要不充分条件;
④若a<0,-1<b<0,则ab>ab2>a.
所有正确命题的序号是 .
①若p、q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件;
②若p为:存在x∈R,x2+2x+2≤0,则p为:任意x∈R,x2+2x+2>0;
③已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q成立的必要不充分条件;
④若a<0,-1<b<0,则ab>ab2>a.
所有正确命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①判断充分性是否成立,再判定必要性是否成立,由此判断正误;
②特称命题“存在x∈R,p(x)”的否定是“对任意x∈R,¬p(x)”,由此判断正误;
③判断充分性是否成立,再判定必要性是否成立,即得判断正误;
④由不等式的性质即可判断正误.
②特称命题“存在x∈R,p(x)”的否定是“对任意x∈R,¬p(x)”,由此判断正误;
③判断充分性是否成立,再判定必要性是否成立,即得判断正误;
④由不等式的性质即可判断正误.
解答:
解:①由于“p且q为真”,则p、q必全为真命题,
由于“p或q为真”,则p、q至少有一个真命题,
则“p且q为真”是“p或q为真”的充分不必要条件,故①不正确;
②若p为:存在x∈R,x2+2x+2≤0,则┐p为:任意x∈R,x2+2x+2>0,故②正确;
③已知p是r的充分不必要条件,则p⇒r为真命题,r⇒p为假命题,
由于s是r的必要条件,则r⇒s为真命题,
又由q是s的必要条件,则s⇒q为真命题,
那么p是q成立的充分不必要条件,故③不正确;
④由于a<0,-1<b<0,则ab>0,0>ab2>a,故④正确.
故答案为:②④
由于“p或q为真”,则p、q至少有一个真命题,
则“p且q为真”是“p或q为真”的充分不必要条件,故①不正确;
②若p为:存在x∈R,x2+2x+2≤0,则┐p为:任意x∈R,x2+2x+2>0,故②正确;
③已知p是r的充分不必要条件,则p⇒r为真命题,r⇒p为假命题,
由于s是r的必要条件,则r⇒s为真命题,
又由q是s的必要条件,则s⇒q为真命题,
那么p是q成立的充分不必要条件,故③不正确;
④由于a<0,-1<b<0,则ab>0,0>ab2>a,故④正确.
故答案为:②④
点评:本题以命题为载体,考查命题的真假判断,理解定义,掌握必要的解题方法是解题的关键,综合性强.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
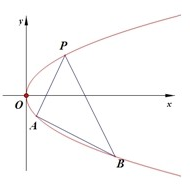 如图,抛物线的方程为y2=2px(p>0).
如图,抛物线的方程为y2=2px(p>0).