题目内容
(1)当 时,等式
时,等式
是否成立? 呢?
呢?
(2)假设 时,等式
时,等式 成立.
成立.
能否推得 时,等式也成立?
时,等式也成立? 时等式成立吗?
时等式成立吗?
 时,等式
时,等式
是否成立?
 呢?
呢?(2)假设
 时,等式
时,等式 成立.
成立.能否推得
 时,等式也成立?
时,等式也成立? 时等式成立吗?
时等式成立吗?成立,证明见答案
(1)当 时,等式成立.当
时,等式成立.当 时,左边
时,左边 ,右边
,右边 ,左边
,左边 右边,等式不成立.
右边,等式不成立.
(2)假设 时等式成立,即有
时等式成立,即有
 ,而
,而

 时等式成立.
时等式成立.
但 时,
时, ;
;
 时,
时, .
.
故 时等式均不成立.
时等式均不成立.
 时,等式成立.当
时,等式成立.当 时,左边
时,左边 ,右边
,右边 ,左边
,左边 右边,等式不成立.
右边,等式不成立.(2)假设
 时等式成立,即有
时等式成立,即有 ,而
,而
 时等式成立.
时等式成立.但
 时,
时, ;
;  时,
时, .
.故
 时等式均不成立.
时等式均不成立.
练习册系列答案
相关题目
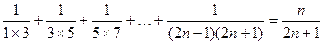 (n∈N*)
(n∈N*) .
. 与Sn+1的大小,并说明理由.
与Sn+1的大小,并说明理由. 满足
满足 且
且
 .
.
 ;
;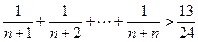 的过程中,由k推导到k+1时,不等式左边增加的式子是
的过程中,由k推导到k+1时,不等式左边增加的式子是 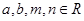 ,且
,且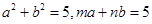 ,则
,则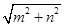 的最小值为
的最小值为 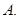
 ,求
,求 的最大值
的最大值 ,由
,由 到
到 ,不等式左端变化的是 ( )
,不等式左端变化的是 ( ) 一项
一项 和
和 一项
一项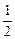 ,an+1=
,an+1= ,则a2,a3,a4,a5的值分别为_________,由此猜想an=_________.
,则a2,a3,a4,a5的值分别为_________,由此猜想an=_________.