题目内容
用数学归纳法证明不等式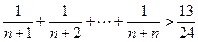 的过程中,由k推导到k+1时,不等式左边增加的式子是
的过程中,由k推导到k+1时,不等式左边增加的式子是
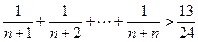 的过程中,由k推导到k+1时,不等式左边增加的式子是
的过程中,由k推导到k+1时,不等式左边增加的式子是 
求 即可
即可
当 n=k时,左边 ,
,
n=k+1时,左边 ,
,
故左边增加的式子是 ,即
,即
 即可
即可当 n=k时,左边
 ,
,n=k+1时,左边
 ,
,故左边增加的式子是
 ,即
,即

练习册系列答案
相关题目
题目内容
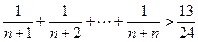 的过程中,由k推导到k+1时,不等式左边增加的式子是
的过程中,由k推导到k+1时,不等式左边增加的式子是 
 即可
即可 ,
, ,
, ,即
,即
