题目内容
2.一直线l过直线l1:3x-y=3和直线l2:x-2y=2的交点P,且与直线l3:x-y+1=0垂直.(1)求直线l的方程;
(2)若直线l与圆心在x正半轴上的半径为$\sqrt{2}$的圆C相切,求圆C的标准方程.
分析 (1)联立两个直线解析式先求出l1和l2的交点坐标,然后利用直线与直线l3垂直,根据斜率乘积为-1得到直线l的斜率,写出直线l方程即可;
(2)利用圆心到直线的距离等于半径,求出圆心坐标,即可求圆C的标准方程.
解答 解:(1)直线l1:3x-y=3和直线l2:x-2y=2的交点P(0.8,-0.6),
设直线l的方程x+y+c=0,代入P,可得0.8-0.6+c=0,∴c=-0.2,
∴设直线l的方程x+y-0.2=0;
(2)设圆心坐标为(a,0)(a>0),则$\frac{|a-0.2|}{\sqrt{2}}=\sqrt{2}$,∴a=2.2,
∴圆C的标准方程(x-2.2)2+y2=2.
点评 本题考查直线与圆的方程,考查直线与直线、直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.已知1,x,y,z,9成等比数列,则y=( )
| A. | -3 | B. | 3 | C. | 5 | D. | ±3 |
11.某市家庭煤气的使用量xcm3和燃气费f(x)(元)满足关系$f(x)=\left\{\begin{array}{l}C,0<x≤A\\ C+B({x-A}),x>A\end{array}\right.$,已知某家庭今年前三个月的燃气费如表:
若四月份该家庭使用了20cm3的煤气,则其燃气费为11.5元.
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4元 |
| 二月份 | 25m3 | 14元 |
| 三月份 | 35m3 | 19元 |
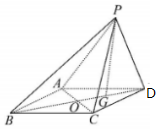 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.