题目内容
12.已知函数f(x)=|x-1|-|2x+m|,m∈R.(1)当m=-4时,解不等式f(x)<0;
(2)当x∈(1,+∞)时,f(x)<0恒成立,求m的取值范围.
分析 (1)分类讨论解不等式,即可得出结论;
(2)x∈(1,+∞)时,f(x)<0,即x-1<|2x+m|,即可求m的取值范围.
解答 解:(1)当m=-4时,f(x)=|x-1|-|2x-4|,
x<1时,不等式可化为1-x+2x-4<0,∴x<3,∴x<1;
1≤x≤2时,不等式可化为x-1+2x-4<0,∴x<$\frac{5}{3}$,∴1≤x<$\frac{5}{3}$,
x>2时,不等式可化为x-1+4-2x<0,∴x>3,∴x>3,
综上所述,不等式的解集为{x|x<$\frac{5}{3}$或x>3};
(2)x∈(1,+∞)时,f(x)<0,即x-1<|2x+m|,
∴m>-x-1或m<1-3x,
∴m≥-2.
点评 本题主要考查带由绝对值的函数,绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
4.a=log20.7,b=($\frac{1}{5}$)${\;}^{\frac{2}{3}}$,c=($\frac{1}{2}$)-3,则a,b,c的大小关系是( )
| A. | c>b>a | B. | b>c>a | C. | c>a>b | D. | a>b>c |
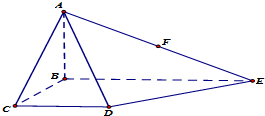 如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.
如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.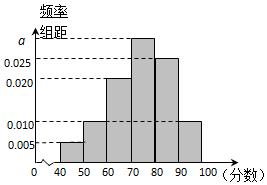 某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.