题目内容
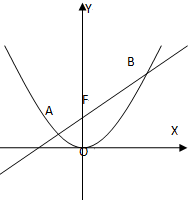 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.(Ⅰ)证明:∠AOB为钝角.
(Ⅱ)若△AOB的面积为4,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)设直线l的方程为:y=kx+1,联立
,得x2-4kx-4=0,设直线l与抛物线的交点坐标A(x1,y1),B(x2,y2),由x1x2+y1y2=-3<0,证明∠AOB为钝角.
(Ⅱ) 由(I)知:|AB|=
=4(k2+1),O到直线AB的距离d=
,由此利用三角形的面积能求出直线方程.
|
(Ⅱ) 由(I)知:|AB|=
| (1+k2)[(4k)2-4×(-4)] |
| 1 | ||
|
解答:
(I)证明:依题意设直线l的方程为:y=kx+1(k必存在),
联立
,得x2-4kx-4=0,
∵△=16k2+16>0,
∴设直线l与抛物线的交点坐标A(x1,y1),B(x2,y2),
则有x1x2=-4,y1y2=
=1,
∴x1x2+y1y2=-3<0,
依向量的数量积定义,cos∠AOB<0,
∴∠AOB为钝角.
(Ⅱ)解:由(I)知:|AB|=
=4(k2+1),
O到直线AB的距离d=
,
∴S△AOB=
|AB|d=2
=4,
解得k=±
,
∴直线方程为y=
x+1,y=-
x+1.
联立
|
∵△=16k2+16>0,
∴设直线l与抛物线的交点坐标A(x1,y1),B(x2,y2),
则有x1x2=-4,y1y2=
| x12 |
| 4 |
| x22 |
| 4 |
∴x1x2+y1y2=-3<0,
依向量的数量积定义,cos∠AOB<0,
∴∠AOB为钝角.
(Ⅱ)解:由(I)知:|AB|=
| (1+k2)[(4k)2-4×(-4)] |
O到直线AB的距离d=
| 1 | ||
|
∴S△AOB=
| 1 |
| 2 |
| k2+1 |
解得k=±
| 3 |
∴直线方程为y=
| 3 |
| 3 |
点评:本题考查角为钝角的证明,考查直线方程的求法,解题时要认真审题,注意椭圆弦长公式的合理运用.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
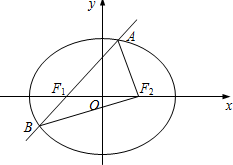 如图,椭圆E:
如图,椭圆E: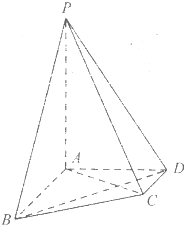 在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=
在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=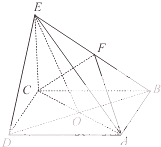 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.