Question

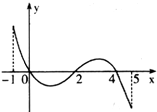已知函数f（x）的定义域为[-1，5]，部分对应值如图：

x	-1	0	4	5
f（x）	1	2	2	1

f（x）的导函数y=f′（x）的图象如图所示，下列关于f（x）的命题：
①函数f（x）是周期函数； 
②函数f（x）在[0，2]是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最小值为0；
④函数y=f（x）-a的零点个数可能为0、1、2、3、4个．
其中正确命题的序号是

 

．

Answer 1

考点：命题的真假判断与应用,利用导数研究函数的单调性

专题：函数的性质及应用

分析：由导函数的图象看出函数的单调区间及原函数的极值点，结合函数f（x）在定义域[-1，5]内的部分对应值表，可以作出函数f（x）图象的大致形状，由图象形状可以判断四个命题的真假．

解答： 解：①由函数图象可知函数不具备周期性，故①错误．
②由导数图象可知，当-1＜x＜0或2＜x＜4时，f′（x）＞0，函数单调递增，
当0＜x＜2或4＜x＜5，f′（x）＜0，函数单调递减，
所以当x=0和x=4时，函数取得极大值f（0）=2，f（4）=2，
当x=2时，函数取得极小值f（2）=0，
所以f（x）的极小值为0，故②正确．
③若当x∈[-1，t]时，f（x）的最大值是2，则0≤t≤5，
故t的最小值为0，故③正确．
④∵f（-1）=1，f（0）=2，f（4）=2．f（5）=1，
∴根据函数的单调性和极值，做出函数的图象如图，（线段只代表单调性），根据题意函数的极小值不确定，分f（2）＜1或1≤f（2）＜2两种情况，由图象知，函数y=f（x）和y=a的交点个数有0，1，2，3，4等不同情形，所以④正确
故答案为：②③④

点评：本题考查导数知识的运用，考查导函数与原函数图象之间的关系，正确运用导函数图象是关键．