题目内容
14.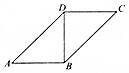 如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.
如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.
分析 先确定三棱锥A-BCD的外接球直径为AC,再根据图中数据求出外接球的半径R,从而求得体积.
解答 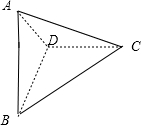 解:四边形ABCD中,∠ABD=∠BDC=90°,
解:四边形ABCD中,∠ABD=∠BDC=90°,
∴AB⊥BD,CD⊥BD;
∵沿BD折成直二面角A-BD-C,如图所示;
∴AB⊥平面BCD,CD⊥平面ABD,
∴AB⊥BC,CD⊥DA;
∴三棱锥A-BCD的外接球的直径为AC,
且|AC|2=|AB|2+|BD|2+|CD|2=102+102+102=300
∴外接球的半径为R=5$\sqrt{3}$,它的体积为$\frac{4π}{3}$•${(5\sqrt{3})}^{3}$=500$\sqrt{3}$π.
故答案为:500$\sqrt{3}$π.
点评 本题考查了几何体外接球的体积计算问题,解题的关键是确定外接球的直径.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体的体积是( )
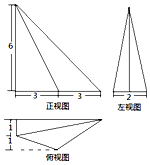

| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
3.在△ABC中,M是BC的中点,BM=2,AM=AB-AC,则△ABC的面积的最大值为( )
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | $3\sqrt{3}$ |