为了响应国家发展足球的战略.哈市某校在秋季运动会中.安排了足球射门比赛．现有10名同学参加足球射门比赛.已知每名同学踢进的概率均为0.6.每名同学有2次射门机会.且各同学射门之间没有影响．现规定:踢进两个得10分.踢进一个得5分.一个未进得0分.记X为10个同学的得分总和.则X的数学期望为( )A．30B．40C．60D．80 题目和参考答案——青夏教育精英家教网——

题目内容

4．为了响应国家发展足球的战略，哈市某校在秋季运动会中，安排了足球射门比赛．现有10名同学参加足球射门比赛，已知每名同学踢进的概率均为0.6，每名同学有2次射门机会，且各同学射门之间没有影响．现规定：踢进两个得10分，踢进一个得5分，一个未进得0分，记X为10个同学的得分总和，则X的数学期望为（　　）

A．

30

B．

40

C．

60

D．

80

分析每位同学的进球个数ξ～B（2，0.6），可得E（X）=10×5E（ξ）．

解答解：每位同学的进球个数ξ～B（2，0.6），
可得E（ξ）=2×0.6=1.2．
∴E（X）=10×5E（ξ）=50×1.2=60．
故选：C．

点评本题考查了二项分布列的概率与数学期望计算公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

孟建平各地期末试卷汇编系列答案

蓉城学堂中考总复习点击与突破系列答案

中考导航模拟卷系列答案

本土教辅名校作业系列答案

常青藤英语完形填空与阅读理解系列答案

蓝卡中考试题解读系列答案

中考新动向系列答案

一考通综合训练系列答案

新课程指导与练习系列答案

中考阶段总复习模拟试题系列答案

相关题目

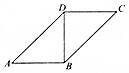如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD，现将四边形ABCD沿BD折成直二面角A-BD-C，则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm³．

15．如果执行如图所示的程序框图，那么输出的k=5．

12．设椭圆$E：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的右顶点为A，右焦点为F，B为椭圆E在第二象限上的点，直线OB交椭圆E于点C，若直线FB平分线段AC，则椭圆E的离心率是$\frac{1}{2}$．

19．设S_n为等比数列{a_n}的前n项和，a₃=8a₆，则$\frac{S_4}{S_2}$的值为（　　）

9．设T_n为数列{a_n}的前n项之积，即T_n=a₁a₂a₃…a_n-1a_n，若${a_1}=2，\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n-1}}-1}}=1$，当T_n=11时，n的值为10．

16．已知a，b，c为正实数，且a+b+c=3
（Ⅰ）解关于c的不等式|2c-4|≤a+b；
（Ⅱ）证明：$\frac{c^2}{a}+\frac{a^2}{b}+\frac{b^2}{c}≥3$．

13．已知数列{a_n}为等比数列，且${a_{2015}}+{a_{2017}}=\int_0^2{\sqrt{4-{x^2}}}dx$，则a₂₀₁₆（a₂₀₁₄+a₂₀₁₈）的最小值为$\frac{{π}^{2}}{2}$．

14．已知集合A={x|x²-2x-3＜0}，$B=\{\;x|\frac{1}{x}＜1\;\}$，则A∩B=（　　）

{x|-1＜x＜0或0＜x＜3}

{x|-1＜x＜0或1＜x＜3}