题目内容
关于x2+y4=1所表示曲线的描述:
(1)该曲线是中心对称图形;
(2)该曲线是轴对称图形;
(3)点p(cosθ,sinθ)可能在该曲线外部;
(4)该曲线围成的图形的面积小于或等于π;
(5)该曲线围成的图形的面积一定大于π,
以上说法正确的是: (只需填上正确命题的题号)
(1)该曲线是中心对称图形;
(2)该曲线是轴对称图形;
(3)点p(cosθ,sinθ)可能在该曲线外部;
(4)该曲线围成的图形的面积小于或等于π;
(5)该曲线围成的图形的面积一定大于π,
以上说法正确的是:
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:由函数中心对称和轴对称的判定方法判断(1),(2);由-1≤sinθ≤1同时把点的坐标代入判断(3);求出曲线所围成的曲线的面积范围判断(4).
解答:
解:对于曲线x2+y4=1:
(1)以-x换x,以-y换y,曲线方程不变,该曲线是中心对称图形,(1)正确;
(2)以-x换x,曲线方程不变,该曲线是轴对称图形,(2)正确;
(3)∵cos2θ+sin4θ≤cos2θ+sin2θ=1,点p(cosθ,sinθ)不可能在该曲线外部,(3)错误;
由已知曲线的方程可得:y4=1-x2≥0⇒x2≤1⇒-1≤x≤1,同理可推得-1≤y≤1,
即曲线围在由直线x=±1,y=±1所确定的正方形内,故曲线是封闭的.
又对比圆的方程x2+y2=1可知圆上的任一点(x,y)应在相应的方程x2+y4=1表示的曲线内部(除去与坐标轴的交点),
故其面积应大于圆的面积π,
故(4)错误;(5)正确.
故答案为:(1)(2)(5).
(1)以-x换x,以-y换y,曲线方程不变,该曲线是中心对称图形,(1)正确;
(2)以-x换x,曲线方程不变,该曲线是轴对称图形,(2)正确;
(3)∵cos2θ+sin4θ≤cos2θ+sin2θ=1,点p(cosθ,sinθ)不可能在该曲线外部,(3)错误;
由已知曲线的方程可得:y4=1-x2≥0⇒x2≤1⇒-1≤x≤1,同理可推得-1≤y≤1,
即曲线围在由直线x=±1,y=±1所确定的正方形内,故曲线是封闭的.
又对比圆的方程x2+y2=1可知圆上的任一点(x,y)应在相应的方程x2+y4=1表示的曲线内部(除去与坐标轴的交点),
故其面积应大于圆的面积π,
故(4)错误;(5)正确.
故答案为:(1)(2)(5).
点评:本题考查曲线方程知识,由方程研究曲线的性质,是中档题.

练习册系列答案
相关题目
设Sn是等差数列{an}的前n项和,已知a5=9,S2=4,则a2=( )
| A、1 | B、2 | C、3 | D、5 |
在△ABC中,
=(cos18°,sin18°),
=(2cos63°,2cos27°)则面积为( )
| AB |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
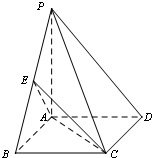 如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,点E为PB的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,点E为PB的中点.