题目内容
12.已知函数y=f(x),若对于任意x∈R,f(2x)=2f(x)恒成立,则称函数y=f(x)具有性质P,(1)若函数f(x)具有性质P,且f(4)=8,则f(1)=2;
(2)若函数f(x)具有性质P,且在(1,2]上的解析式为y=cosx,那么y=f(x)在(1,8]上有且仅有3个零点.
分析 (1)根据性质P的条件,利用方程关系进行递推即可.
(2)根据性质P的条件,分别求出函数的解析式,利用函数零点的定义解方程即可.
解答 解:(1)因为函数y=f(x),具有性质P,
所以对于任意x∈R,f(2x)=2f(x)恒成立,
所以f(4)=f(2×2)=2f(2)=2f(2×1)=4f(1)=8,
所以f(1)=2.
(2)若函数y=f(x)具有性质P,且在(1,2]上的解析式为y=cosx,
由y=cosx=0,则x=$\frac{π}{2}$,
由f(2x)=2f(x)得f(x)=2f($\frac{x}{2}$),
若2<x≤4,则1<$\frac{x}{2}$≤2,则f(x)=2f($\frac{x}{2}$)=2cos$\frac{x}{2}$,
则函数f(x)在(2,4]上的解析式为y=2cos$\frac{x}{2}$,
由2cos$\frac{x}{2}$=0,得x=π,
若4<x≤8,则2<$\frac{x}{2}$≤4,则f(x)=2f($\frac{x}{2}$)=4cos$\frac{x}{4}$,
在(4,8]上的解析式为y=4cos$\frac{x}{4}$,
由y=4cos$\frac{x}{4}$=0得x=2π,
所以y=f(x)在(1,8]上有且仅有3个零点,分别是$\frac{π}{2}$,π,2π.
故y=f(x)在(1,8]上有且仅有3个零点,
故答案为:2,3
点评 本题主要考查抽象函数的应用,利用定义进行递推以及求出函数的解析式是解决本题的关键.考查学生的运算和推理能力.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
3.下列结论①(sinx)′=-cosx;②$(\frac{1}{x})'=\frac{1}{x^2}$;③$({log_3}x)'=\frac{1}{3lnx}$;④$({x^2})'=\frac{1}{x}$.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
7.若a+2b=1(ab≠0),下列结论中错误的是( )
| A. | ab的最大值为$\frac{1}{8}$ | B. | $\frac{1}{ab}$的最小值为8 | ||
| C. | a2+ab+b2的最小值为$\frac{1}{4}$ | D. | $\frac{1}{{{a^2}+ab+{b^2}}}$的最大值为4 |
17.函数f(x)=2x+3x-7的零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
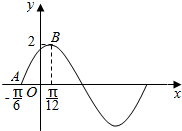 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示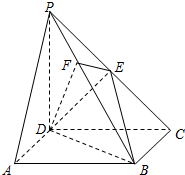 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. (1)计算:${27^{\frac{2}{3}}}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+2lg({\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}})$
(1)计算:${27^{\frac{2}{3}}}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+2lg({\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}})$