题目内容
7.若a+2b=1(ab≠0),下列结论中错误的是( )| A. | ab的最大值为$\frac{1}{8}$ | B. | $\frac{1}{ab}$的最小值为8 | ||
| C. | a2+ab+b2的最小值为$\frac{1}{4}$ | D. | $\frac{1}{{{a^2}+ab+{b^2}}}$的最大值为4 |
分析 根据特殊值法,代入判断即可.
解答 解:∵a+2b=1,故a,b至少有1个为正数,
(1)a,b同时为正数时,能取到最大值,
由a+2b=1≥2$\sqrt{2ab}$,得:2ab≤$\frac{1}{4}$,ab≤$\frac{1}{8}$,
故A正确;
(2)显然ab<0时,比如a=-1,b=1,$\frac{1}{ab}$=-1,最小值不是8,
故B错误;
(3)a2+ab+b2=(1-2b)2+(1-2b)b+b2=3${(b-\frac{1}{2})}^{2}$+$\frac{1}{4}$≥$\frac{1}{4}$,
故C、D正确,
故选:B.
点评 本题考察了基本不等式的性质,注意性质应用满足的条件,本题是一道基础题.

练习册系列答案
相关题目
18.已知$sinα=\frac{{\sqrt{5}}}{5}$且α是锐角,tanβ=-3,且β为钝角,则α+β的值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
16.已知一个多面体的内切球的半径为3,多面体的表面积为15,则此多面体的体积为( )
| A. | 45 | B. | 15 | C. | 3π | D. | 15π |
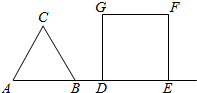 如图所示,A、B、D、E四点在同一直线上,△ABC是边长为2的正三角形,DEFG是边长为2的正方形,在静止状态时,B点在D点的左侧,且$|{\overrightarrow{BD}}|=1$,让A点沿直线AB从左到右运动,当A点运动到E点时,运动结束.
如图所示,A、B、D、E四点在同一直线上,△ABC是边长为2的正三角形,DEFG是边长为2的正方形,在静止状态时,B点在D点的左侧,且$|{\overrightarrow{BD}}|=1$,让A点沿直线AB从左到右运动,当A点运动到E点时,运动结束.